完全贝叶斯均衡

---

以英国牧师贝叶斯(T·Bayes，1702～1761)的名字命名的概念，完全贝叶斯均衡是所有参与人战略和信念的一种结合，它满足如下条件：
❶ 在给定每个人有关其他人类型的信念的情况下，他的战略选择是最优的；
❷ 每个人有关他人类型的信念都是使用贝叶斯法则从所观察到的行为中获得的。

完全贝叶斯均衡的要点在于当事人要根据所观察到的他人的行为来修正自己有关后者类型的"信念"(主观概率)，并由此选择自己的行动。这里，修正过程使用的是贝叶斯规则。

这一点意味著，每个参与人都假定其他参与人选择的是均衡战略。

用形式化的语言来描述，完全贝叶斯均衡可以定义如下：

假定有n个参与人，参与人i的类型是θ_i∈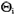_i，θ_i是私人信息，p_i(θ_－i|θ_i)是属于类型θ_i的参与人i认为其他n－1个参与人属于类型θ_－i=(θ₁，…θ_i－1，θ_i+1，…，θ_n)的先验概率。令S_i是i的战略空间，s_i∈S_i是一个特定的战略(依赖于类型θ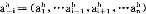_i)，a_i=(a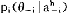，…a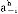#_－1，a₊₁，…a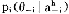)是在第h个信息集上参与人i观测到的其他n－1个参与人的行动组合，它是战略组合s_－i=(s₁，…s_i－1，s_i+1，…s_n)的一部分(即s_－i规定的行动)，p_i(θ_－i|a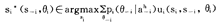_i)是在观测到a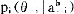_i的情况下参与人i认为其他n－1个参与人属于类型θ_－i=(θ₁，…θ_i－1，θ_i+1，…，θ_n)的后验概率，p_i是所有后验概率p_i(θ_－i|a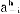_i)的集合(即p_i包括了参与人i在每一个信息集h上的后验概率)，u_i(s_i，s_－i，θ_i)是i的效用函数。

完全贝叶斯均衡是一个战略组合s^*(θ)=(s₁^*(θ₁)，…，s_n^*(θ_n))和一个后验概率组合p=(p₁，…，p_n)，满足：

(P)对于所有的参与人i，在每一个信息集h，

s_i^*(s_－i，θ_i)∈argmax∑p_i(θ_－i|a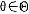_i)u_i(s_i，s_－i，

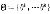θ_i)

(B)p_i(θ_－i|a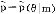_i)是使用贝叶斯法则从先验概率p_i(θ_－i|θ_i)，观测到的a#_i和最优战略s－i(·)得到(在可能的情况下)。