在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
注意 定理和推论的前提条件“同圆或等圆”必不可少.
比如:大小不等的圆中可以有相等的圆心角,但所对的弧、所对的弦不一定相等.
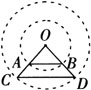
两个同心圆中,同样的圆心角所对弦AB≠ CD,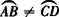 .
.
例1 在☉O中,如果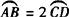 ,那么弦AB与CD之间有( ).
,那么弦AB与CD之间有( ).
A.AB<2CD
B.AB=CD
C.AB>2CD
D.不能确定
答 A.
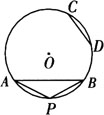
[解析] 如图,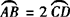 ,取
,取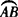 的中点P,则
的中点P,则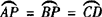 .
.
∴AP=BP=CD,在△ABP中,AB
例2 已知:☉O中,AB、CD是两条非直径且相等的弦.
求证:两条弦的弦心距(圆心到弦的距离)相等.
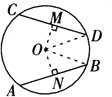
证明 过O点分别作OM⊥CD于M点ON⊥AB于N点,连接OB、OD.
∵AB=CD,根据垂径定理.
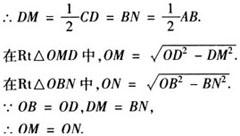
[解析] 圆心角同弧、弦之间关系定理的推论可以推广为:圆心角、弦、弧、弦心距之间的关系定理,如果两个圆心角,两条弧,两条弦,两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
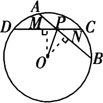
例3 如图,☉O的两条弦AB、CD相交于点P,且OP平分∠BPD.
求证: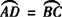 .
.
证明 过O点作OM⊥CD于M点.
作ON⊥AB于N点.
∵OP平分∠BPD,
∴OM=ON.
∴AB=CD.
∴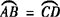 .
.
∴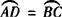 .
.
- 莫曳皆部是什么意思
- 莫曳靺鞨是什么意思
- 莫曼德人是什么意思
- 莫替古人担忧是什么意思
- 莫替古人耽忧是什么意思
- 莫有是什么意思
- 莫朗是什么意思
- 莫朗根之战是什么意思
- 莫望是什么意思
- 莫望中州叹黍离,元和圣德要君诗是什么意思
- 莫木克是什么意思
- 莫札特是什么意思
- 莫朴是什么意思
- 莫来是什么意思
- 莫来头是什么意思
- 莫来头;没来头是什么意思
- 莫来拦我球门路。是什么意思
- 莫松夏热沟是什么意思
- 莫松达坂是什么意思
- 莫构得是什么意思
- 莫林胡兀儿是什么意思
- 莫林,j.-y.是什么意思
- 莫枚士是什么意思
- 莫树国是什么意思
- 莫树杰是什么意思
- 莫格人是什么意思
- 莫桑比克是什么意思
- 莫桑比克人民共和国是什么意思
- 莫桑比克人民共和国国徽是什么意思
- 莫桑比克人民共和国国旗是什么意思
- 莫桑比克人民共和国国歌是什么意思
- 莫桑比克人民共和国宪法是什么意思
- 莫桑比克人民共和国首都是什么意思
- 莫桑比克人民议会是什么意思
- 莫桑比克共和国(莫桑比克)是什么意思
- 莫桑比克内战是什么意思
- 莫桑比克暖流是什么意思
- 莫桑比克武装力量是什么意思
- 莫桑比克民族解放战争是什么意思
- 莫桑比克海峡是什么意思
- 莫桑比克海流是什么意思
- 莫桑比克解放阵线党是什么意思
- 莫桑比克部长会议是什么意思
- 莫桑比克银行是什么意思
- 莫桑比克(莫桑比克)是什么意思
- 莫梦弼是什么意思
- 莫梭普是什么意思
- 莫棠是什么意思
- 莫森数是什么意思
- 莫棱棱子是什么意思
- 莫榮新是什么意思
- 莫欺零落残牙齿,曾吃红绫饼餤来。是什么意思
- 莫止《昭君曲》是什么意思
- 莫正形是什么意思
- 莫正民起义是什么意思
- 莫此为甚是什么意思
- 莫此之甚是什么意思
- 莫比尔是什么意思
- 莫比尔公司是什么意思
- 莫比尔湾之战是什么意思