高斯函数gaosi hanshu

函数[x]，对任何实数x,[x]表示不超过x的最大整数. 例如 [5. 3]=5,[π]=3,[-4]=-4,[-1.5]=-2.
由定义容易推出函数 [x]的一些简单性质：
❶x-1< [x]≤x,[x]≤x<[x]+1. 这个性质与定义等价.

❷ [ n+x] =n+ [x]，其中n是整数.
证 设x= [x] +a,0≤a<1，于是n+x=n+[x]+a，由定义得 [n+x]=n+ [x].

❸ [x]+ [y]≤ [x+y].
证 设x= [x] +a,y= [y] ]=β,0≤a,β<1，于是x+y=[x]+[y]+α+β，但0≤α+β<2，从而[a+β] =0或1，由性质
❷可得 [z+y] = [x] +[y]+[α+β]，于是 [x+y]=[x]+[y]或 [x+y] = [x]+ [y ] +1.
利用函数[x]的性质，可以证明含有高斯函数的恒等式. 例如，设n是任意给定的实数，n是正整数，

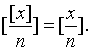
则
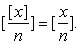
证 令[x/n ]=a，则由性质❶知，a≤x/n例 证明含 [x]的不等式，对任何整数x,y，都有 [2x]+ [2y]≥ [x]+ [x+y]+ [y].
证 含x=m+α,y=n+β，其中0≤α,β<1，于是 [x]=m,[y]=n. [2x]=2m+ [2a],[2y]=2n+[2β],[x+y]=m+n+[α+β]. 因此为证明原不等式，只须证明 [2α]+[2β]≥ [α+β] . 由于α,β∈ [0,1)，因而只须分别四种情况对所要证明的不等式一一验证即可. 这四种情况是：
❶0≤α<1/2,0≤β<1/ 2 ;
❷0≤α<1/2,1/2≤β<1;
❸1/2≤β<1,0≤β<1 / 2;
❹1/2≤α<1,1/2≤β<1. 经验证，所要证的不等式均成立，故原不等式成立.
下面举例说明如何解含 [x]的方程式. 例如，若N是一个正整数，问方程x²-[x²]=(x-[x])²在区间1 ≤ x ≤ N中有多少个解？ (1982年瑞典数学竞赛试题)首先，若x为 [1,N]上的任一整数，则它显然是原方程的一个解. 为了求出原方程的非整数解，设x′=m+a，其中02+2ma+a²一 [m²+2ma+a²] =a²，即2ma= [2ma+a²]. 因为上式右端是一个整数，所以等式左端也必须是一个整数，根据性质
❷，这时[2ma+a²]=2ma+ [a²] =2ma. 也就是说，x=m+a是原方程的解，当且仅当2ma是整数，故当

这2m-1个值时，x=m+a都是原方程的解，又m可取1,2，…，N-1，故非整数解的个数为

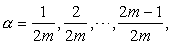
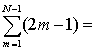
(N-1)2.

. 因此原方程的解数为N+ (N-1)²＝N²-N+1.

☚ 数论函数 　 n!的质因数分解 ☛