频数分布frequency distribution

指变量值按大小分组后，各个组段内变量值个数（频数）的分布。如测得1982年某市120名12岁男孩身高(cm)，将身高值分组后，归纳各个组段的个数，即得频数分布表。据此可以了解频数分布的规律。可以利用频数分布表，以加权法或简捷法计算均数及标准差，并可制作频数分布图。

频数分布

[参]频数表

频数分布frequency distribution

亦称“次数分布”。对原始数据资料按一定标志分组，并按一定顺序排列，同时列出各组的总体单位数。

按工人的产量分组（件）	50|70	70|90	90|110	110|120	合计
组中值	60	80	100	115
工人人数（频数）	100	540	300	60	1000
各组工人比重(%)（频率）	10	54	30	6	100

编制频率分布，一般是先将原始数据资料按其标志由小到大或由大到小排成序列，然后将序列资料进行归类分组，列出各组的总体单位数。各组的单位数称为频数或次数； 用百分数表示的相对频数叫频率。下表为某工厂工人生产某种产品日产量的频率分布。频数分布可以反映总体单位在各组的分布情况。可用图形来表示。常用的频数分布图有频数直方图和频数多边形图。直方图由一系列的长方形构成。各长方形的底代表各组的组距，画在横轴上；各长方形的高代表各组的频数，用纵轴上单位数表示。将直方图中各长方形上边的中点依次连接起来所形成的折线图形，称为频数多边形。图形两端应引至外侧组中点与横轴基线相接。如果所考察的随机变量为连续随机变量，那么按此做出的图就是频率曲线。常见的频率分布有： 对称分布、V形分布 （又称反众数分布） 和J形分布。

频数分布Frequency Distribution

见“统计分布”。

频数分布

对一个随机事件作重复观察，其中某变量值出现的次数称频数； 将各变量值及其相应的频数列表为频数分布表，简称频数表，如表1。若将变量值分组，则某组段包含的变量值个数称频数，将各组段及其相应的频数列表为频数表，如表2第(1)、(3)栏。由频数表可绘制频数分布图。表1“每家患者数”属离散变量，故绘条图，见图1；表2“身高”属连续变量，故绘直方图，见图2。

表1 每家某病患者数

每家患者数	家庭数
0 1 2 3 4 5	20 80 40 50 10 10

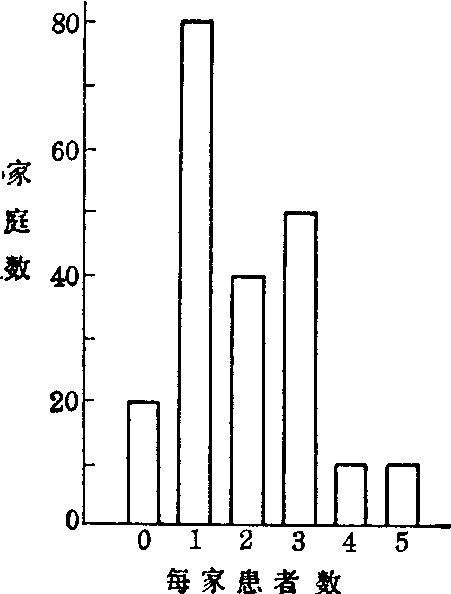
图1 每家某病患者数分布
1. 编制频数表的步骤如下：
(1) 找出最大、最小值，计算极差。
(2) 定组段数。根据研究目的及观察例数确定组段数。一般100例上下，可分10组左右，例数多，可分细些，即组段数多些，反之粗些，即组段数少些。为计算用，组段数可适当增多，以减少计算误差；为显示分布特征，则组段数不宜太多或太少。
(3)定组距。相邻两组段下限值之差称组距。各组段的组距可相等，也可不等。相等组距可用“极差/组数”估计。为便于分组，组距常取整数。

表2 某市12岁男童120人的身高(cm)分布

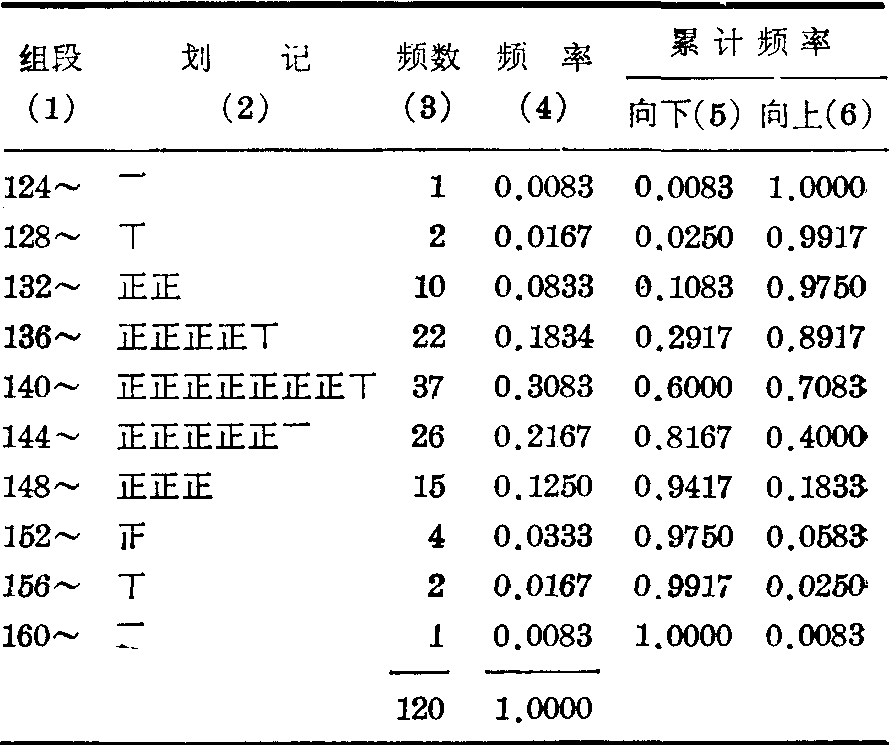
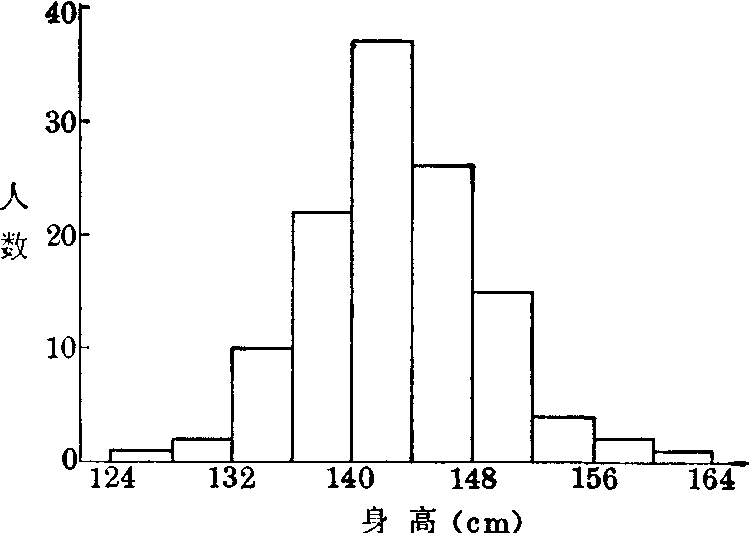
图2 某市12岁男童120人的身高分布

(4)定组段。各组段的最小值称下限，相邻较大组段的下限即本组段的上限。第一组段应包括最小观察值，末组段应包括最大观察值。
(5) 计频数。用分卡法或划记法，得出各组段的频数。例 某市12岁男童120人的身高(cm)如下，试编制频数表。

142.3 134.5 145.2 151.1 141.2 143.5 134.7 150.8 125.9 160.9 134.7 129.4 132.1 143.6 142.4

156.6 148.8 141.8 144.0 141.5 139.2 147.3 144.5 132.7 154.2 138.5 142.5 145.9 150.0 148.9

142.7 134.4 146.8 145.4 148.8 144.7 138.1 137.1 152.9 137.9 138.9 141.2 146.7 143.3 146.7

145.7 148.8 135.1 146.2 140.1 139.3 140.2 147.1 147.9 139.9 137.7 148.9 144.0 146.5 139.2

138.2 137.9 150.3 143.3 150.6 141.9 137.4 142.9 141.8 149.7 138.5 154.0 135.5 149.0 139.6

141.6 151.3 133.1 156.3 139.5 147.8 145.1 134.9 141.4 147.5 139.6 147.7 144.4 142.1 142.4

142.5 140.8 142.7 141.9 146.4 140.5 145.8 143.6 140.9 136.9 143.5 152.3 143.4 140.2 138.7

130.5 149.8 143.9 140.7 143.8 138.9 147.9 142.3 141.4 148.1 142.9 146.6 137.4 145.4 139.9

最大值为160.9，最小值为125.9，极差=160.9-125.9=35.0。取10组左右，组距=35.0/10=3.5，取4cm。组段、划记、计频数的结果见表2第(1)～(3)栏。
2. 频数分布的用途：
(1)提供分组数据，以便进一步计算与分析。
(2)揭示观察值的分布类型，以便选择适当统计方法，
进行计算与分析。Karl Pearson曾提出13种频数分布型的方程及其特征。医学科研中最常见的频数分布型有正态分布、正偏态分布等。正态分布型如儿童身高值、成人红细胞数、成人血清总蛋白量等。表2和图2显示近似正态分布，其高峰在“140～”cm组段，可按正态分布原理作统计处理。正偏态分布型如正常成人血铅含量及食物中毒潜伏时间等。表1、图1是以每家1例患者为高峰的正偏态分布。偏态分布资料可用非参数法作统计处理，有的可用变量变换，使其正态化后，再按正态分布处理。
(3) 便于发现某些特大或特小的可疑值，必要时经检验后舍弃。
(4)样本含量足够大时，以频率作为概率的估计值。如表2第(4)栏系第(3)栏各组段频数除以总频数的商，称频率或相对频数。用以估计该市12岁男童身高为各组段数值的概率，各组段频率之和应等于1。将各组段频率自上而下（或自下而上）依次累加，得累计频率，如表2第(5)、(6)栏，用以估计身高小于各组段上限（或大于各组段下限）的概率。

频数分布

又称次数分布。根据研究目的，选择一定的标志对所研究的舆论现象进行分组，然后将总体中的所有单位按组归类整理，就形成了总体中总体单位数在各组间的频数分布。分布在各组的总体单位数叫频数，也称做次数。各组的频数与总次数的比率称为成数，也叫频率。把总体中各分组与其频数顺序编排而成的数列，就是频数分布数列，简称分布数列。分布数列具有重要的认识作用，通过编制频数分布数列，可以观察总体内部的次数分布状况、比例关系及其变化发展的趋势。同时，它还是进一步进行描述分析的基础。

频数分布

又称次数分布。是在统计分组的基础上，将各个体按组归类整理所形成的个体数量在各组间的分布情况。

频数分布frequency distribution

亦称“次数分布”。对原始数据资料按一定标志分组，并按一定顺序排列，同时列出各组的总体单位数。编制频数分布，一般是先将原始数据资料按其标志由小到大或由大到小排成序列(array)，然后将序列资料进行归类分组，列出各组的总体位数。各组的单位数称为频数或次数；用百分数表示的相对频数叫做频率。下表为某工厂工人生产某种产品日产量的频数分布。

按工人日产量 分组（件）	组中值	工人人数 （频数）	各组工人 比重(%) （频率）
50～60 60～70 70～80 80～90 90～100 100～110 110～120 合计	55 65 75 85 95 105 115	40 60 240 300 220 80 60 1000	4 6 24 30 22 8 6 100

频数分布可以反映总体单位在各组的分布情况。
频数分布也可以用图形来表示，常用的频数分布图有频数直方图(frequency histogram)和频数多边形图(frequency polygon)。直方图由一系列的长方形构成。各长方形的底代表各组的组距，画在横轴上；各长方形的高代表各组的频数，用纵轴上单位数表示。将直方图中各长方形上边的中点依次连接起来所形成的折线图形，称为频数多边形图。图形两端应引至外侧的组中点与横轴基线相接。
根据上述频数分布资料，可绘制频数直方图和频数多边形图如下：

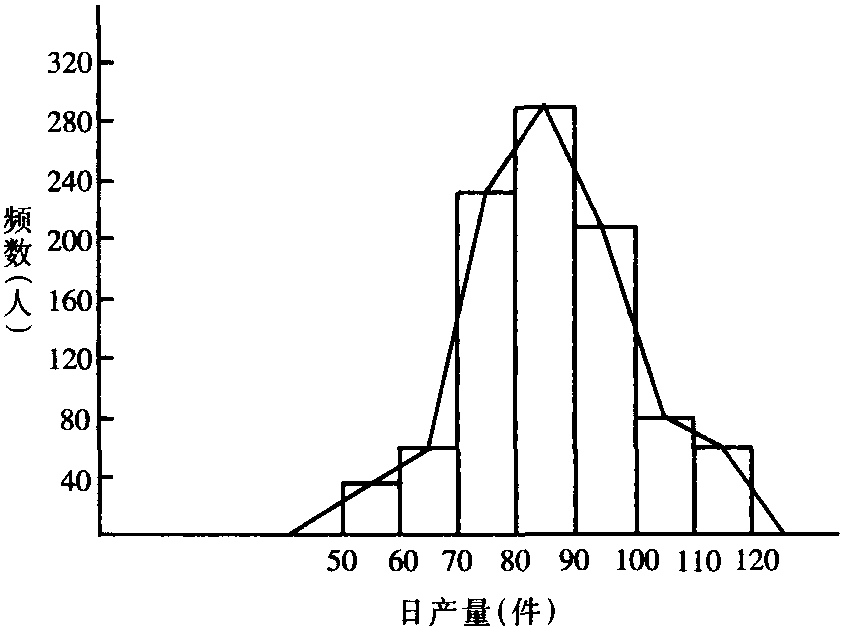
频数分布图可以更直观、更形象地反映数据资料的分布情况。