间接证法jianjie zhengfa

亦称间接证明.间接证法不是直接证明论题的真实性，而是通过证明论题的否定不真，或证明与论题等价的另一命题的真实性，从而断定论题为真的证明方法.
中学数学教学中常用的间接证法有：对偶法、反证法、同一法、穷举归谬法、穷举法等.
❶对偶法 代替论题a→b，而去证明与之等价的逆否命题b→a的方法.

❷ 反证法 a→b的否定式为

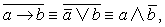
由

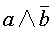
出发进行推理，如果发生矛盾，表明

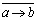
为假，

从而可知a→b为真.这种证明a→b为真的方法，叫做反证法.

❸同一法 只适用于论题的题设、题断所指的对象是存在唯一的情形.其步骤是：先设法构造出符合论题题断的对象，再证明所构造的对象确有题设所述的性质，但是符合题设、题断的对象都是唯一存在的，可知所构造出的对象与题设所指的对象是同一个，从而断定论题成立.这种证法叫同一法，它常用于几何证明问题.

❹穷举归谬法 用反证法证明命题a→b为真时，依上述对反证法的解释，而去证明a∧→0为真.如果此时包括多种情况，难以一概而论作出证明.不妨设＝b₁∨b₂∨…∨b_m.如若能证明出a∧b_i→0(i=1,2，…，m)都为真，也就证明了a∧b→0为真.这种证明方法叫做穷举归谬法.事实上，当a∧b_i→0(i=1,2，…，m)都为真时，a∧b_i(i=1,2，…，m)都为假，即a∧b_i≡0. 那末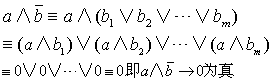

❺穷举法 若有一组真命题a_i→b_i(i=1,2，…，m),a₁,a₂，…，a_m是问题的所有可能的情况，b₁,b₂，…，b_m互不相容，则可断定它们的逆命题b_i→a_i(i=1,2，…，m)都为真，而这些逆命题恰是所要证明的原论题，这种证明方法叫做穷举法.