绳索中的张力
绳索中的张力shengsuo zhong de zhangli
在张紧的绳索上某位置作一假想横截面,由假想横截面分开的绳的两部分互相施加的绳内拉力。
如图,在绳子A、B两端分别施以拉力F的F′,设想在绳子内部C处作一横截面,把绳子分成两部分,截面两侧即出现张力Tc和Tc′。Tc与Tc′等值反向。再将绳子D处也作一横截面,在其两侧也出现张力TD和TD′。CD段绳所受张力为Tc′和TD。根据牛顿第二定律,则有Tc′-TD =ma。
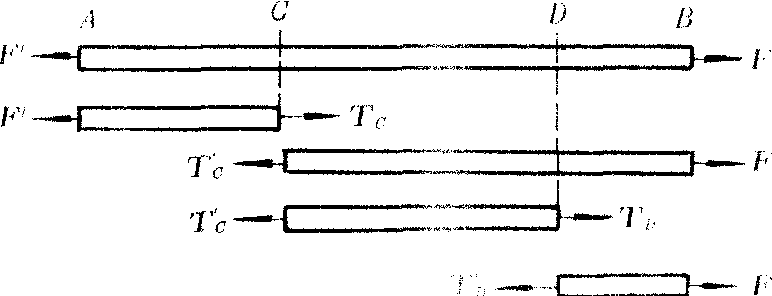
由式可知CD段绳质量m≠0,加速度a≠0时,则张力Tc′与TD大小不相等。当CD段绳质量m=0,即绳很轻,可忽略其质量时,则张力Tc′与 TD大小相等。当a=0,即绳处于静止或匀速直线运动时,则|Tc′|=|TD|。这说明,绳子作加速运动而它的质量不可忽视时,绳子内部各截面处的张力不同;只有这段绳子的质量可以忽略不计或沿绳的方向无加速度时,绳的各截面处张力的大小才相等。
☚ 弹性体形变 弹性体的拉伸压缩形变 ☛
- 三门峡水电站是什么意思
- 三门峡甘山国家森林公园是什么意思
- 三门峡的传说是什么意思
- 三门峡秦墓是什么意思
- 三门峡立交桥西汉墓是什么意思
- 三门峡统计年鉴是什么意思
- 三门峡虢国墓地是什么意思
- 三门峡黄河公路大桥是什么意思
- 三门干部是什么意思
- 三门李轶闻是什么意思
- 三门柜是什么意思
- 三门柱是什么意思
- 三门栈道是什么意思
- 三门桩是什么意思
- 三门江国家森林公园是什么意思
- 三门湾是什么意思
- 三门犯人是什么意思
- 三门生是什么意思
- 三门白波发运司是什么意思
- 三门白波辇运司是什么意思
- 三门白波都监是什么意思
- 三门白波黄渭河水路发运使是什么意思
- 三门街前后传是什么意思
- 三门走狗是什么意思
- 三门运渠是什么意思
- 三门里面千层阁,万井中心一朵山。是什么意思
- 三闲集是什么意思
- 三间是什么意思
- 三间一套房是什么意思
- 三间临水屋,半树夕阳山。是什么意思
- 三间四耳是什么意思
- 三间四耳倒八尺是什么意思
- 三间屋子两头住——谁也瞒不了谁是什么意思
- 三间庐是什么意思
- 三间张是什么意思
- 三间排是什么意思
- 三间瓦屋是什么意思
- 三间老屋是什么意思
- 三间草堂是什么意思
- 三闺媛词合集是什么意思
- 三闾是什么意思
- 三闾大夫是什么意思
- 三闾小玉是什么意思
- 三闾庙是什么意思
- 三闾庙 - 唐·戴叔伦是什么意思
- 三闾投汨罗是什么意思
- 三闾桥是什么意思
- 三闾氏是什么意思
- 三闾祠 - 清·查慎行是什么意思
- 三闾魂是什么意思
- 三防是什么意思
- 三防小组是什么意思
- 三防峡是什么意思
- 三防技术是什么意思
- 三防抢救力量是什么意思
- 三防抢救队是什么意思
- 三防指示是什么意思
- 三防措施是什么意思
- 三防教育夏令营是什么意思
- 三防消毒车是什么意思