线性消费系统
线性消费系统Linear Consumption System
消费者对各种商品的支出与商品价格和消费者收入成线性函数关系的系统。是在对数效用函数的特殊情况下,由效用极大化一阶条件导出的。在两种商品情形下,给定消费者对数形式的效用函数:
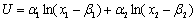
x1>β1,x2>β2
消费者预算线为:p1x1+p2x2=m
效用极大化的一阶条件为: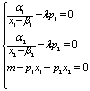
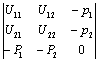
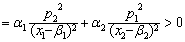
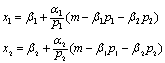
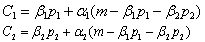
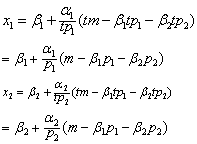
☚ 理性预期 埃奇沃思盒状图 ☛
- 毌丘俭讨高句骊是什么意思
- 毌丘兴是什么意思
- 毌丘甸是什么意思
- 毌將是什么意思
- 毌終是什么意思
- 毌部是什么意思
- 毌(母)部是什么意思
- 母是什么意思
- 母丁簋浮雕是什么意思
- 母丁香是什么意思
- 母丁香膏是什么意思
- 母不传丑是什么意思
- 母不赖歪是什么意思
- 母与女是什么意思
- 母与妻是什么意思
- 母与子是什么意思
- 母与子 [法国]罗曼·罗兰是什么意思
- 母丘儉平高句麗斷碑是什么意思
- 母丛是什么意思
- 母主家庭是什么意思
- 母之怀抱,为饮几乳是什么意思
- 母乖蚰子是什么意思
- 母乙是什么意思
- 母也天只,不谅人只是什么意思
- 母乳是什么意思
- 母乳化牛乳是什么意思
- 母乳喂养是什么意思
- 母乳喂养宣传日是什么意思
- 母乳喂养的好处是什么意思
- 母乳性黄疸是什么意思
- 母乳黄疸是什么意思
- 母亲是什么意思
- 母亲、孩子、人民的英雄是什么意思
- 母亲(之一)是什么意思
- 母亲(之二)是什么意思
- 母亲之歌(选录) [智利]米斯特拉尔是什么意思
- 母亲会是什么意思
- 母亲保护神是什么意思
- 母亲原型是什么意思
- 母亲和儿子是什么意思
- 母亲和女儿是什么意思
- 母亲和子女是什么意思
- 母亲和我是什么意思
- 母亲喂养是什么意思
- 母亲因儿子显贵而显贵是什么意思
- 母亲在召唤是什么意思
- 母亲学校是什么意思
- 母亲对子女的教育是什么意思
- 母亲对子女的爱是什么意思
- 母亲居室是什么意思
- 母亲恐惧是什么意思
- 母亲慈爱是什么意思
- 母亲或妻子的娘家是什么意思
- 母亲或祖母去世是什么意思
- 母亲救女儿算不算“见义勇为”是什么意思
- 母亲教女有方是什么意思
- 母亲教子为官清廉是什么意思
- 母亲教子勤学是什么意思
- 母亲死是什么意思
- 母亲水窖项目是什么意思