线性插值法xianxingchazhifa

求函数近似值的一种方法.设函数y=f(x)，在区间〔x₁,x₂〕上有定义，且已知y₁＝f(x₁),y₂＝f(x₂).为了确定x₁,x₂之间一数x′的函数值f(x′)，在区间〔x1,x₂〕上用一次函数

近似代替函数y=f(x)进行计算，得f(x′)的近似值.这种求函数近似值的方法叫做线性插值法.

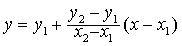
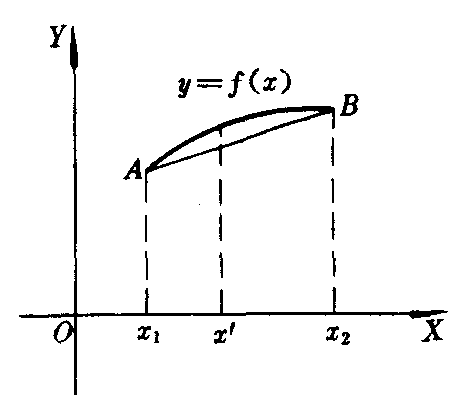
线性插值法的几何意义是在点A(x₁,y₁)和点B(x₂,y₂)之间用直线近似地代替曲线（如图）.x₁和x₂两点距离越小，所得f(x′)的近似值精确度越高.
由于一次函数的值容易算出，因此这种方法有实用意义.在使用函数表求函数值时，可以利用这种方法确定在表中不曾列出的函数值.
例如，利用指数函数e^x表求e^0.627.在表中可以查到e^0.62=1.8589和e^0.63＝1.8776.若查不到e^0.627，则在区间〔0.62,0.63〕上，将函数y=e^x的关系式用一次函数

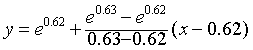
近似代替，将x=0.627代入，得

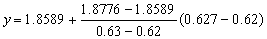
　=1.8720.
即e^0.627＝1.8720.