移动平均MA(q)

在q阶移动平均过程中，每个观察值是由随机干扰项及其滞后到q期的加权平均而产生，我们记这种过程为MA(q)。其方程如下：

y_t＝μ+ε_t-θ₁ε_t-1-θ₂ε_t-2-…-θ_qε_t-q

(1)

其中参数θ₁，…，θ_q可以是正数也可以是负数。
过程y_t的平稳性要求特征方程
θ(B)=1-θ₁B-θ₂B²-…-θ_qB^q＝0的根必须都落在单位圆之外。
在移动平均模型中，假定随机扰动项是独立同分布，即由白噪声生成。特别地，假定每个扰动项ε_t是均值为0，方差为σ_ε²的正态随机变量，且协方差γ_k＝cov(ε_t,ε_t-k)=0，对任意k≠0成立。白噪声过程的加权和却可提供非白噪声过程的很好表达。这样，过程MA(q)可由刚好q+2个参数描绘：均值μ，扰动项方差σ_ε²和确定移动平均权数的参数θ₁，…，θ_q。
q阶移动平均过程的方差，
Var(y_t)=γ₀＝E[(y_t-μ)²]
＝E(ε_t²+θ₁²ε_t-1²+…+θ_q²ε_t-q²-2θ₁ε_tε_t-1-…)
＝σ_ε²+θ₁²σ_ε²+…+θ_q²σ_ε²
＝σ_ε²(1+θ₁²+θ₂²+…+θ_q²)

(2)

q阶移动平均过程仅有q期的记忆力，它的非零自相关系数有q个，记作ρ_k(k =1，…，q)，由下式给出：

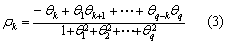
所以，样本自相关函数可用于确定移动平均过程的阶数（假定所关心的时间序列是由移动平均过程产生）。MA(q)的自相关函数ρ_k有q个非零数，当k>q时ρ_k为0。