直线相关与回归的关系

直线相关与回归是研究两变量间直线关系的两种统计方法。直线相关用相关系数r说明直线关系的方向和密切程度； 而直线回归用直线回归方程描述两变量变化的数量关系，其中回归系数b，说明X每变动一个单位，Y平均变动的单位数。直线相关与回归虽有区别，但又互相联系。区别
(1)在资料要求上，相关要求两变量X、Y都是随机变量，如正常人的血清胆固醇和动脉壁胆固醇含量，两者都不能预先指定；回归要求Y是随机变量，而X可以是随机变量，亦可以是一般变量，即可以指定，如毒理实验中，选定某毒物的几个浓度，测定各浓度对数与死亡率的概率单位的关系。
(2)在意义上，相关反映相互关系； 回归反映依存关系。
(3) 在应用上，说明变量间的相关程度用相关；说明两现象间变化的数量关系用回归。
联系
(1) 同一资料的r、b正负号相同。如r为正，说明X增大（或减小）,Y亦增大（或减小）; b为正，说明X增加（或减少）一个单位，Y平均增加（或减少）b个单位。
(2) r的假设检验(检验假设H₀为总体相关系数ρ=0)与b的假设检验(检验假设为总体回归系数β=0) 均用t检验，统计量t值的计算公式不同，但同一资料的数值相等，即t_r＝t_b，故结论相同，因而可用r的假设检验（直接查表）代替b的假设检验，较为简便。
(3) r与b可以相互转换。

式中l_XX、l_YY分别为变量X、Y的离均差平方和，lXY为变量X、Y的离均差积和，b_Y.X为由X推Y的回归方程之回归系数，bX.Y为由Y推X的回归方程之回归系

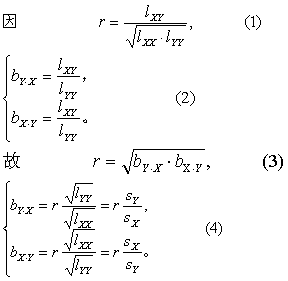
秩 次		Y的累计
X 1 2 3 4.5 4.5 6	Y 1 2.5 2.5 4 5 6	秩次个数 5 3 3 1 1 0

Y的第一个秩次是1，其下有5个比它大，故秩次个数为5; Y的第二个秩次为2.5，下面有3个比它大，故秩次个数为3;Y的第四个秩次为4，与它对应的X秩次是4.5，它下面的一个秩次也是4.5，所以第4个秩次个数记为1而不是2。这样处理的依据是，当分析X与Y的相关时，X变Y不变或X不变Y变，均属无相关。
(3) 按式(3)计算r_K值。

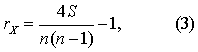
式中n为样本含量。
对r_k进行ρ_X＝ 0的假设检验，只需将算得的r_X按n查表2(r_K界值表)得P值，再按所取检验水准作出推断结论。
r_K的校正： 当相同秩次较多时，可用下式计算校正等级相关系数r′_K

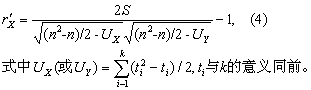
例2 试对例1资料用Kendall等级相关系数作分析。

表4 rK计算表

公社编号 (1)	秩 次		Y的累计 秩次个数 (4)
	黄曲霉毒素相 对含量，X (2)	肝癌死亡率 (1/10万),Y (3)
4 2 3 1 5 6 7 8 9 10	1 2 3 4 5 6 7 8 9 10	3 2 1 7 4 9 6 5 10 8	7 7 7 3 5 1 2 2 0 0
			34 (S)

H₀: ρ_X＝0,
H₁: ρ_K≠0。
a=0.05。
将X的秩次按自然数排列并计算Y的累计秩次个数见表4第(4)栏。

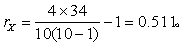
按n=10查表2，得0.05>P>0.01，按a=0.05水准拒绝H₀，结论同例1。

---

直线相关与回归的关系

直线相关与回归是研究两变量间直线关系的两种统计方法。直线相关用相关系数r说明直线关系的方向和密切程度； 而直线回归用直线回归方程描述两变量变化的数量关系，其中回归系数b，说明X每变动一个单位，Y平均变动的单位数。直线相关与回归虽有区别，但又互相联系。区别
(1)在资料要求上，相关要求两变量X、Y都是随机变量，如正常人的血清胆固醇和动脉壁胆固醇含量，两者都不能预先指定；回归要求Y是随机变量，而X可以是随机变量，亦可以是一般变量，即可以指定，如毒理实验中，选定某毒物的几个浓度，测定各浓度对数与死亡率的概率单位的关系。
(2)在意义上，相关反映相互关系； 回归反映依存关系。
(3)在应用上，说明变量间的相关程度用相关；说明两现象间变化的数量关系用回归。
联系
(1) 同一资料的r、b正负号相同。如r为正，说明X增大（或减小）,Y亦增大（或减小）; b为正，说明X增加（或减少）一个单位，Y平均增加（或减少）b个单位。
(2) r的假设检验 (检验假设H₀为总体相关系数ρ=0)与b的假设检验(检验假设为总体回归系数β=0)均用t检验，统计量t值的计算公式不同，但同一资料的数值相等，即t_r＝t₀，故结论相同，因而可用r的假设检验（直接查表）代替b的假设检验，较为简便。
(3) r与b可以相互转换。

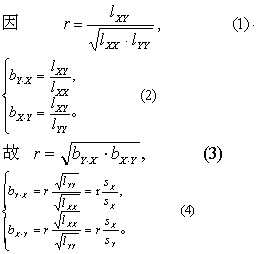
式中l_XX、l_YY分别为变量X、Y的离均差平方和，l_XY为变量X、Y的离均差积和，b_Y、X为由X推Y的回归方程之回归系数，b_X.Y为由Y推X的回归方程之回归系数，s_X、s_Y分别为变量X、Y的标准差。
(4)相关与回归可相互解释。由式(1)并参见条目“直线回归”式(4)得

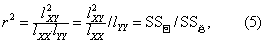
故 SS_回＝r²SS_总,(6)
又 SS总=SS回+SS剩。(7)
从式(5)～(7)可见：
❶式(5)中r²是相关系数的平方，又称决定系数，即采用回归后Y方面减少的平方和SS_回与总平方和SS_总的比值。结合式(7)可知，r²≤1，故|r|≤1。一个资料，其SS_总是固定的，相关愈密切则r²愈大，由式(6)可见SS_回也就愈大，表示回归效果愈好。
❷再由式(7)可见，SS_回大，误差SS_剩就小。因此医学研究中常引入回归来减小误差。如体重变异较大，而身高与体重关系密切，引入由身高推算体重的回归方程，得各身高的体重，变异就大为减小。
❸有时，两变量间经假设检验有相关，但相关系数较小，这时虽引入回归，但由于减少的误差太小，所以无实际意义。如n=100,r=0.2，引入回归后，
SS_回＝(0.2)²SS_总＝0.04SS_总
减少的误差仅为SS总的4%，因此实际意义不大。