传递函数

---

一种以系统参数表示的线性定常系统的输入量与输出量之间关系的数学表达式。

线性定常系统传递函数的定义是：当初始条件为零时，输出量(亦称为响应函数)的拉普拉斯变换与输入量(亦称为驱动函数)的拉普拉斯变换之比。

设有一个线性定常系统，它的微分方程是：

a₀Y⁽ⁿ⁾+a₁Y(^n－1)+…+a_n－1Y⁽¹⁾+a_nY

=b₀X^m+b₁X^(m－1)+…+b_m－1X⁽¹⁾+b_mX(n>m)

式中，X，Y分别是系统的输入量和输出量；X_(m)；Y⁽ⁿ⁾分别是X，Y的m级和n级导数；b_m，a_n(m=1，2，…，m；n=1、2…，n)是微分方程的系数。初始条件为零时，对方程两端进行拉普拉斯变换，就可以得到该系统的传递函数

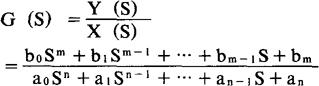
传递函数表达了系统本身的特性，而与输入量或驱动函数无关。

传递函数分母中S的最高阶数，等于输出量最高导数的阶数。如果S的最高阶数等于n，则这个系统便称为n阶系统。