洛伦兹变换
洛伦兹变换luolunzi bianhuan
两个作相对运动的惯性系之间的相对论性时空坐标变换。适用于各种运动速度的情况。其在低速下的近似,就是伽利略变换。设惯性系κ静止,其时空坐标为(t、x、y、z)。另一惯性系κ′的时空坐标为(t′、x′、y′、z′)。κ′系的x′轴与κ系的x轴重合。y′、z′轴分别与y、z轴平行。κ′系以速度v沿x轴相对于κ系作匀速直线运动。在κ′系原点与κ系原点重合的一瞬间,校准分别静止于二系的钟,使t=t′=0。于是洛伦兹变换为
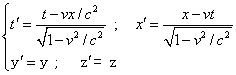
☚ 狭义相对论 同时的相对性 ☛
洛伦兹变换
狭义相对论中,把两个彼此相对作匀速直线运动的惯性参考系中的时间和空间坐标联系起来的数学变换。
- 波爱修是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特是什么意思
- 波特万是什么意思
- 波特中短篇小说集是什么意思
- 波特列索夫是什么意思
- 波特吉特是什么意思
- 波特和劳勒的综合激励模式是什么意思
- 波特夫是什么意思
- 波特夫是什么意思
- 波特夫,赫利斯托是什么意思
- 波特尔奇是什么意思
- 波特尔奇是什么意思
- 波特斯是什么意思
- 波特普通式竞争策略是什么意思
- 波特,威是什么意思
- 波特,科是什么意思
- 波特,诺是什么意思
- 波状压条是什么意思
- 波狄卡斯是什么意思
- 波玉温是什么意思
- 波珀先生的企鹅是什么意思
- 波瓦尔宁阅读者守则是什么意思
- 波的图象是什么意思
- 波的尼亚湾是什么意思
- 波的干涉是什么意思
- 波的衍射是什么意思
- 波皮万诺夫是什么意思
- 波秋斯是什么意思
- 波稜是什么意思
- 波立特是什么意思
- 波立特是什么意思
- 波立特选集是什么意思
- 波立谷是什么意思
- 波粒二象性是什么意思
- 波粒二象性是什么意思
- 波粒二象性是什么意思
- 波粒佯谬·生命与复合时空是什么意思
- 波粱诺夫是什么意思
- 波索什可夫是什么意思
- 波级是什么意思
- 波纳文图拉是什么意思
- 波纹喇叭是什么意思
- 波纹管气胎加压装置及计算是什么意思
- 波纹角胫叶甲是什么意思
- 波维纳是什么意思
- 波缅洛夫斯基小说选是什么意思
- 波缘大参是什么意思
- 波缘大参是什么意思
- 波缘楤木是什么意思