波的描述bo de miaoshu

物理学中，通常由下列基本概念对波进行描述。
❶波面、波前、波射线：波传播过程中，沿波的传播方向各点的振动位相依次落后，由振动位相相同的点（位相差为零）所组成的面叫波面。波面就是波动的同相面。离波源最远亦即“最前方”的波面叫做波前，又称波阵面。对一个确定的波动来说，在任何时刻波前的位置都是确定的，并且都只有 一个波前，而波面有无限多个。任何时刻波前上各点的振动位相都等于波源在开始振动时刻的位相。在各向同性均匀介质中，与波面垂直且表明波传播方向的射线叫波射线，简称波线。
❷平面波、球面波、柱面波：真实波动过程的理想模型。按照波面的形状，波可分为平面波、球面波、柱面波等等。波面是平面的波叫平面波。平面波的波面是一系列平行的平面，波射线是互相平行的直线。例如沿弹性直杆的轴向传播的纵波，在管中传播的声波，射到地面上的太阳光波都是平面波。波面是球面的波叫球面波。波源的形状大小比起传播的距离来，可以忽略不计时称为点波源。点波源在各向同性均匀介质中激发的波是球面波。球面波的波面是以点波源为心的同心球面。波射线是相交于点波源的射线。在远离球面波中心的波面局部区域可近似为一平面，因此可以将远离点波源的波看成是平面波，如到达地面的太阳光波。波面为圆柱面的波叫柱面波。在各向同性均匀介质中，由直线波源发出的波就是柱面波，其波面是一系列同轴的圆柱面。
❸波长、波的周期和频率、波数：在波的传播方向上，振动状态相同的相邻两点之间的距离叫波长，用λ表示。由于相邻的振动状态相同的两点位相差为2π，所以波长又可定义为：同一波线上位相差为2π的两点之间的距离。对于横波，波长就是相邻波峰或相邻波谷间的距离。对于纵波，波长就是相邻密部中心之间或者相邻疏部中心之间的距离。在波动过程中，各点作周期性振动，波的传播是振动状态的传播，于是波动过程便形成一定的振动状态在空间的周期性分布，波长正是描写波动的空间周期性的物理量。波动传播一个波长所需要的时间称为波的周期，用T表示。其倒数叫做波的频率，用v表示，v=1/T，波的频率是单位时间内波动前进距离中完整波的数目，或者单位时间内通过波线上某点的完整波的数目。波的频率描述波动在时间上的周期性。波动在时间上的周期性来源于振源振动的时间周期性。波动中振源的某一振动状态在振源的一个振动周期内所传播的距离恰好等于一个波长。因此在一般情况下，波的周期和频率也就与振源振动的周期和频率相同。把波长的倒数1/λ称为波数。波数是在波的传播方向上每单位距离内完整波的数目。在波谱学中常用波数代替频率来描述波的特征。
❹波速：波在单位时间内某一振动状态所传播的距离，用v表示。由于振动状态用位相描述，波速实际上是一定的振动位相的传播速度，因此波速更确切地讲应称为相速。在一个周期内波前进一个波长的距离，所以有v=λ/T=λv。这是波的运动学的一个基本关系式。波长λ表示波在空间的周期性，波的频率v表示波在时间上的周期性，它们通过反映时间和空间关系的物理量波速v而联系起来。机械波波速决定于介质本身的弹性和惯性，即决定于介质的弹性模量和质量密度，与波源的振动频率无关。理论和实验表明，固态介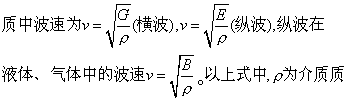
量体密度，G为切变弹性模量，E为杨氏弹性模量，B为容变弹性模量。固体中的杨氏模量大于切变模量，所以固体中纵波的传播速度大于横波的传播速度。对大多数金属材料来说B和G近似看作相等。横波在拉紧的绳中传播的速度为v=，式中T是绳中的张力，ρ是绳子的质量线密度。同一频率的波在不同的介质中波速不同，波长也不同。波速一般还与介质的温度有关。下表给出常见的波速。

❺波矢：表明波的传播方向大小为2π/λ的矢量叫波矢量，简称波矢，用k表示。大小|k|=k=2π/λ又称为圆波数。即波矢的量值等于给定时刻沿波的传播方向每增加单位距离位相滞后2π/λ，波矢与波前垂直，对于平面单色波，波传播方向处处相同，波矢量为一常矢量。以矢量r表示的空间点落后于坐标原点的位相是k·r。相速度用波矢来表示就是v=ω/|k|=ω/k，式中ω为介质质点振动圆频率。波矢在用x射线研究晶体时和在固体能带理论中经常用到。

媒质	波的种类	温度/℃	波速/(ms-1)
空气	纵波	0 20.0 100	331.5 342.4 386
氧气	纵波	0	317.2
水	纵波	13 31	1440 1500
铜	横波	15～20	3570
铁	横波	100	5300
砖	横波	室温	3652