概率的公理化定义gailu de gonglihua dingyi

设Ω是样本空间，ℱ是Ω的一些子集组成的事件域，若ℱ满足下面三条：
❶Ω∈ℱ;
❷若A∈ℱ，则∈ℱ;
❸若A_i∈ℱ (i=1, 2, ………), 有A_i ∈ℱ，则称ℱ为Ω上的σ一代数，称二元组(Ω,ℱ)为具有σ一代数结构的样本空间或称可测空间。
设 (Ω, ℱ)为一可测空间， P是定义在ℱ上的一个实值函数，若满足：
❶对于任意的A∈ℱ，有0≤P (A) ≤1;
❷ P (Ω)=1;
❸对任意的A_i∈ℱ (i=1,2，………)，其中A_i∩A_j＝Φ (i≠J)，恒有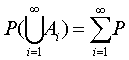(A_i), 则称P为 (Ω, ℱ) 上的概率、 P (A) (A∈ℱ)为事件A的概率，又称三元组 (∮,ℱ , P)为概率空间。这样用公理形式给出的概率定义称为概率的公理化定义。
在概率论中最基本的三个概念就是样本空间Ω，事件域ℱ和概率P。在分析一个随机试验时，我们应该明确它的样本空间，指出所讨论的事件的范围，即事件域，然后确定出概率P, 由此可知，Ω,ℱ, P是描述随机试验的三个基本组成部分。