椭圆的焦点和准线touyuan de jiaodian he zhunxian

直线l₁:x=-a^2/c(或x=-a/e)和l₂:x=a²/c(或分别与椭圆的焦点F₁(-c,0)和F₂(c,0)相对应.
椭圆的焦点和准线有如下性质：
❶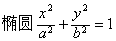上任意一点P到焦点F₁ (或F₂)的距离r₁(或r₂)和到相对应的准线l₁(或l₂)的距离d₁(或d₂)之比等于椭圆的离心率e.

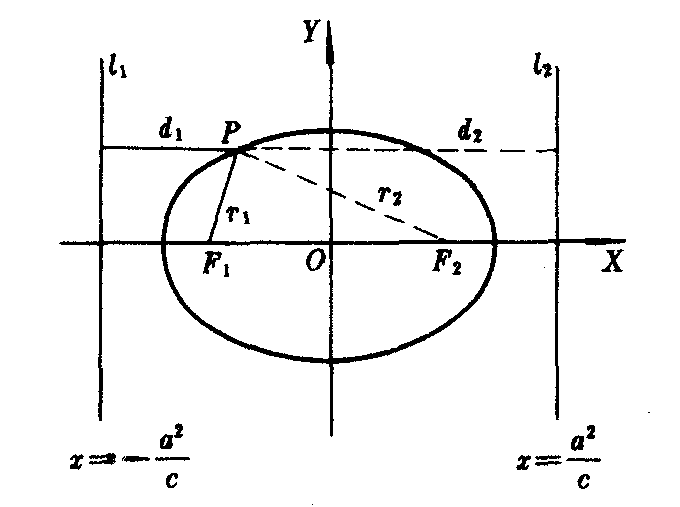
❷设a>c>0，到定点F₁(-c,0) (或F₂(c,0))的距离r₁(或r₂)和到定直线l₁:x=-a^2/c(或l₂:x=a/e)的距离d₁(或d₂)之比等于c/a的点P，必在椭

圆

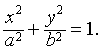
依据这两个性质，可将椭圆定义为：到一个定点的距离和到一条定直线的距离之比等于一个小于1的常数的点的轨迹，这个定点叫做椭圆的（一个）焦点，这条定直线叫做对应于这个焦点的（一条）准线，这个小于1的常数叫做椭圆的离心率.
椭圆方程和焦点坐标、准线方程的对应关系如下表所示.