样本含量估计

抽样研究中，每个样本所包含的调查或受试对象数称为样本含量。在统计研究的抽样设计中要考虑样本含量问题。样本含量过少，所得指标不够稳定，结论也缺乏充分的根据；样本含量过多，会增加实际工作中的困难，对条件的严格控制也不易做到，并且造成不必要的浪费。样本含量估计是在保证研究结论具有一定可靠性的条件下，确定最少的实验或调查单位数。样本含量的估计方法可分为两类：一类是作参数估计时的样本含量估计；另一类是作指标比较时，假设检验中的样本含量估计。
样本含量估计可以通过某些公式计算，也可以查表得到。二者都需要事先确定：
❶第一类错误的概率α，即检验水准。α越小所需样本含量越多。
❷检验效能1-β,β为第二类错误的概率。1-β的意思是备择假设正确时将发现它的能力。如作两样本均数的比较，H0为μ1=μ2,H1为μ1≠μ2，若两样本所代表的总体确有差别，而在100次试验中，平均有95次能发现出差别，则1-β为0.95。检验效能越大，所需样本含量越多。
❸容许误差或差值δ。
❹总体标准差或总体率。α、β和δ根据需要和要求由调查或试验者规定，总体标准差或率可根据前人的类似研究资料或预初试验所得样本标准差或样本率来估计。
统计学家根据某些特定的公式编制了样本含量的便查表，使用简便，但往往仍要结合内插估计，或迳用偏大估计值。本书除举一例外，余均从略，读者需要时可查有关统计专著。下面介绍几种常用的计算法。
参数估计时的样本含量估计
(1) 估计总体均数： 当总体标准差σ已知时按式(1)计算，σ未知时，按式(2)计算。实际工作中σ常属未知，故式(2)常用。

式中n为所需样本含量；δ为容许误差，即对样本均数与总体均数的容许差值，为所求总体均数的(1-a)可信区间间距之半；s为总体标准差的估计值；当确定α后，uα由u界值表查得，tα由t界值表查得，均查本书表中P(2)行，查tα时，一般用自由度ν=∞。将各值代入式(2)，若求得的n较小(如n<30)，或要求准确，可用尝试法（详后）继续求n。如例1。
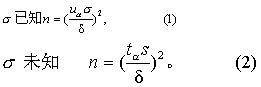
(2) 估计总体率： 当总体率π(π未知时可用样本率p估计)接近0.5(比如0.2～0.8)时，可按照正态近似原理用式(3)计算；否则宜用式(4)计算。式(4)对p作了平方根反正弦变换。式中n为所需样本含量；uα同式(1); p为总体率π的估计值，若同时有几个数值作参考，可取其最接近0.5者，若对总体率一无所知，则可设p=0.5;δ为容许误差；计算时角度单位用度。如例2。
例1 某单位拟用抽样调查了解该地区正常成人白细胞数的平均水平。希望误差不超过100个/mm³。据文献所载，正常成人白细胞数的标准差约1000个/mm3。如取α=0.05，问需调查多少人？
今α=0.05,t0.05,∞=1.96,s=1000个/mm3,δ=100个/mm3，代入式(2)，得

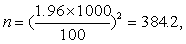
即需调查385人。
例2 现欲用抽样调查了解某地小学生蛔虫感染率。要求误差不超过3%，如取α=0.05，问需调查多少人？
今α=0.05,u0.05=1.96,δ=0.03，设p=0.5。
代入式(3)，得

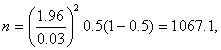
即需调查1068人。
假设检验时的样本含量估计
(1)样本均数与总体均数比较： 单侧检验按式(5)计算，双侧检验按式(6)计算，

式中n为所需样本含量；s为总体标准差的估计值；δ为研究者提出的差值； tα、t_2α及t_2β为α、2α及2β所对应之t值，由t界值表查得(本书均查表中P(2)行)。估算时常要重复上式作多次尝试，每次只更换tα、t_2α及t_2β值：先用自由度v=∞时的t_α、t_2α及t_2β值代入算得n(1); 第二次用v=n(1)-1的t_α、t_2α及t_2β值代入算得n(2); 第三次用v=n(2)-1的tα、t_2α及t_2β值代入算得n(₃)；……；仿此进行，直至前后两次算得结果趋于稳定为止，即为所求样本含量。如例3。
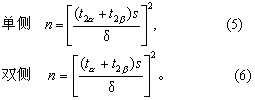
(2) 两样本均数比较： 单侧检验按式(7)计算，双侧检验按式(8)计算。

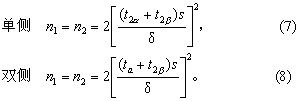
式中n₁和n₂分别为两样本所需含量，一般假定两样本相等； s为总体标准差的估计值；δ为研究者提出的差值；t_α、t_2α及t_2β的意义与尝试法步骤同式(5)及 (6)，但第二次以后的尝试，自由度为前次算得两样本含量之和减2。如例4。
用上法制成不同α、β及δ/σ时所需样本含量便查表如下。
两样本均数比较时所需样本含量

单侧检验α:	0.005			0.01			0.025			0.05
双侧检验α: β:	0.01			0.02			0.05			0.10
	0.05 0.1 0.2			0.05 0.1 0.2			0.05 0.1 0.2			0.05 0.1 0.2
δ/σ
0.35												102
0.40									100		108	78
0.45 0.50			118 96		106	101 82	106	105 86	79 64	108 88	86 70	62 51
0.55		101	79	106	88	68	87	71	53	73	58	42
0.60 0.65 0.70 0.75	101 87 75 66	85 73 63 55	67 57 50 44	90 77 66 58	74 64 55 48	58 49 43 38	74 63 55 48	60 51 44 39	45 39 34 29	61 52 45 40	49 42 36 32	36 30 26 23
0.80 0.85 0.90 0.95 1.00	58 51 46 42 38	49 43 39 35 32	39 35 31 28 26	51 46 41 37 33	43 38 34 31 28	33 30 27 24 22	42 37 34 30 27	34 31 27 25 23	26 23 21 19 17	35 31 28 25 23	28 25 22 20 18	21 18 16 15 14
1.1 1.2 1.3 1.4 1.5	32 27 23 20 18	27 23 20 17 15	22 18 16 14 13	28 24 21 18 16	23 20 17 15 14	19 16 14 12 11	23 20 17 15 13	19 16 14 12 11	14 12 11 10 9	19 16 14 12 11	15 13 11 10 9	12 10 9 8 7
1.6 1.7 1.8 1.9 2.0	16 15 13 12 11	14 13 11 11 10	11 10 10 9 8	14 13 12 11 10	12 11 10 9 9	10 9 8 8 7	12 11 10 9 8	10 9 8 7 7	8 7 6 6 6	10 9 8 7 7	8 7 7 6 6	6 6 5 5 4
2.1 2.2 2.3 2.4 2.5	10 10 9 9 8	9 8 8 8 7	8 7 7 6 6	9 9 8 8 7	8 7 7 7 6	7 6 6 6 5	8 7 7 6 6	6 6 6 5 5	5 5 5 4 4	6 6 5 5 5	5 5 5 4 4	4 4 4 4 3
3.0 3.5 4.0	6 5 5	6 5 4	5 4 4	6 5 4	5 4 4	4 4 3	5 4 4	4 4 3	4 3	4 3	3

摘自 Beyer WH: Handbook of Tables for Probabi-
lity and Statistics,second edition,p 289,CRCPress,Inc.,1979
(3)配对比较（计量资料）: 单侧检验按式(9)计算，双侧检验按式(10)计算，

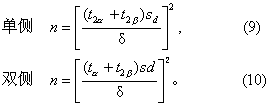
式中n为所需样本对子数； s_d为差值d的标准差之估计值； δ为研究者提出的差值； t_α、t_2α及t₂β的意义与尝试法步骤同式(5)及(6)。但第二次以后的尝试，自由度为前次算得的对子数减1。如例5。
(4)两样本率比较： 单侧检验用式(11)计算，双侧检验用式(12)计算。

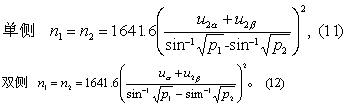
式中n₁和n₂分别为两样本所需含量； p₁及p₂分别为两总体率的估计值；uα 、u₂α及u₂β为α、2α及2β所对应之u值，由u界值表查得(本书均查P(2)行)。如例6。
例3 已知血吸虫病人血红蛋白平均含量为9g/100ml，标准差为2.5g/100ml，现欲研究呋喃丙胺治疗后能否使血红蛋白量增加，规定治疗前后血红蛋白含量升高2g以上者为有效，升高1g以下者为无效；α=0.05,β=0.10，问应治疗多少病人？
本例用单侧检验，δ=2-1=1(g/100ml),s=2.5,2α=0.10,2β=0.20，按式(5)得

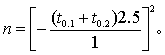
用尝试法，先查t界值表，得t_0.1,∞ =1.645,t_0.2,∞ =1.282，代入上式，得

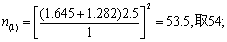
再查t界值表，得t0.1,(5-1)= 1.674 ,t0.2,(54-1)=1.298，再代入前式，得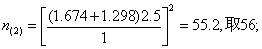

再查t界值表，得t0.1,(56-1)=1.673,t0.2,(56-1)=1.297，再代入前式，得

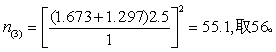
这时n趋于稳定，故可以认为需治疗56个病人。即以56例进行研究，如该药确实有效，则有90%(即1-β)的把握可得出有差别的结论。
例4 在动物镇咳实验中，比较中药复方Ⅰ与复方Ⅱ使小白鼠推迟发生咳嗽的时间，复方Ⅰ平均推迟31.67秒，复方Ⅱ平均推迟44.00秒。设两组标准差相等为25秒，α=0.05,β=0.1，要得出两组有差别的结论，问需用多少只小白鼠作实验。本例用双侧检验，按式(8),δ=44-31.67=12.33 （秒）,s=25秒，α=0.05,2β=0.2，得

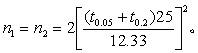
用尝试法。查t界值表，得t0.05,∞=1.960,t0.2,∞ =1.282，代入上式，得

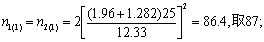
再查t界值表，得t_{0.05,(87×2-2)=1.976},t_{0.2,(87×2-2)=1.287}，代入前式，得

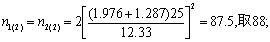
再查t界值表，得t_{0.05(88×2-2)},t_0.2(88×2-2)与前t值接近，故不必继续尝试。
或查上表，双侧检验，α=0.05,β=0.10,δ/σ=12.33/25=0.49，得n≐86。
即每组需用88只小白鼠，两组共需176只。
例5 用某药治疗矽肺病人后，尿矽排出量平均比治疗前增加1.5mg/100ml，其标准差为2.5mg/100ml。假定该药确能使尿矽排出量增加，定α=0.05,β=0.1，问需要观察多少病人才能得出服药前后尿矽排出量有差别的结论？
本例用单侧检验，按式(9),δ=1.5mg/100ml,sd=2.5mg/100ml,2α=0.1,2β=0.2，得

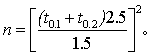
用尝试法。查t界值表，得t0.1,∞=1.645,t0.2,∞ =1.282代入上式，得

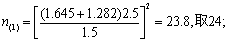
再查t界值表，得t_0.1,(24-1)＝1.714,t_{0.2,(24-1)=1.319}，代入前式，得

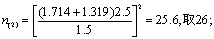
再查t界值表，得t_0.1,(26-1)＝1.708,t_0.2,(26-1) = 1.316，代入前式，得

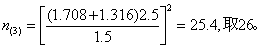
已趋稳定，可取n=26。
例6 用旧药治疗慢性气管炎的近控率，根据过去的经验为20%。现拟试用新药治疗，以旧药治疗为对照。要求新药的近控率须达到40%才值得推广使用。问每组最少要多少病例？(α=0.05,β=0.10)。
本例用单侧检验，按式(11),p₁＝20%,p₂＝40%,2α=0.1,2β=0.2，查u界值表，u0.1=1.645,u_0.2＝1.282，代入得

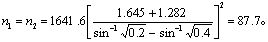
即每组需88例，两组共需176例。