标准差
方差的算术根。常用σ表示,即σ=![]() 。其估计值为Sn=
。其估计值为Sn=![]() 或S=
或S=![]() 。常被应用于测验分数统计中。
。常被应用于测验分数统计中。
标准差standard deviation
统计学上指方差的平方根值。表现一组变数的变异度。其单位与观察值的度量单位相同。样本标准差的表达式为:
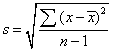
 )2为离均差的平方和,简称平方和;n-1称为自由度。样本标准差是总体标准差的估计值。总体标准差以σ表示。
)2为离均差的平方和,简称平方和;n-1称为自由度。样本标准差是总体标准差的估计值。总体标准差以σ表示。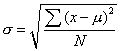
标准差biaozhun cha
差异量数之一。由变异数(又称方差)的平方根得来,故又称均方差。样本标准差用S或SD表示,总体标准量用σ表示。计算标准差的公式是:
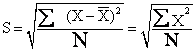
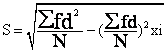
标准差Biaozhuncha
是每个数据与平均数之差的平方的算术平均数的平方根。是表示数据离中趋势的最常用的量数,一般以S表示。计算公式为:
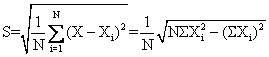
标准差
又称“均方差”。各单位标志值与平均数离差的平方的算术平均数的平方根。测定标志变异度的最主要指标。计算公式为:
![]()
标准差standard deviation
是正态分布的一个总体参数,说明一群变量值的离散情况,计算公式为:
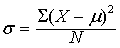
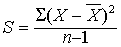
标准差Standard Deviation
亦称“根方差”,或称“均方差”。方差的算术平方根。度量数据分布离散程度的常用方法。标准差越小,数据分布的离散程度越低,分布的集中程度越高。
标准差
方差的平方根。它是衡量一个变量的样本观测值对其平均值的离散程度的指标。参见“方差”。
标准差
又称均方差。是用来反映变量数列的某一数量标志的各项数值距离它的中心值 (或代表值)的差异程度,即离中趋势的一个指标。标准差的大小,不仅取决于标志值的离差程度,还决定于数列平均水平的高低。其计算公式是:
简单平均式:
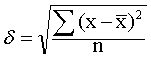
加权平均式:
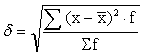
式中:σ代表标准差,x代表变量值,
 代表变量值的算术平均数,n代表变量个数,f代表次数。当标志值很大时,计算标准差通常用简捷法。基本公式是:
代表变量值的算术平均数,n代表变量个数,f代表次数。当标志值很大时,计算标准差通常用简捷法。基本公式是: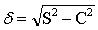
式中,S2代表各标志值对x0的方差,C2代表各标志值对x0的离差的平均数的平方。资料未经分组和已经分组的计算公式分别是:
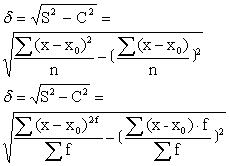
标准差
用期望报酬的标准差来定量分析证券投资风险的一种分析方法。证券投资的风险是指投资报酬变动的可能性,可以用期望报酬的标准差来进行定量分析。显然,某种投资的标准差越大,则说明这种投资的报酬越具变动性,因而投资风险越大。为了计算标准差σ1首先要计算方差。方差是离差平方的加权平均值,权重为相应的概率。方差的计算公式为:
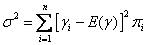
式中σ2为证券的方差,γi为证券在第i事件下的报酬率,E(γ)为证券的期望报酬率,[γi-E (γ)]为离差,πi为事件i的概率。
下面举例说明如何运用标准差计算证券投资的风险。假定某证券分析家认为。某项投资的预期收益和其概率如下(表6—7)。
表6—7 某项投资的预期收益及其概率
| 事件i | 1 | 2 | 3 | 4 | 5 | 6 |
| 概率πi | 0. 15 | 0. 20 | 0. 25 | 0. 25 | 0.20 | 0. 05 |
| 预期报酬γi | 1. 50 | 1. 60 | 1. 70 | 1.80 | 1. 90 | 2.00 |
那么根据上表可计算出预期报酬的期望值E(r)
E(γ)=0.15×1.50+0.20×1.60+0.25××1.70+0.25×1.80+0.10×1.90+0.05×2.00=1.71
预期报酬期望值是可能实现的收入值,但由于各种因素。实际报酬与预期报酬之间可能存在差异,这种差异可用标准差来反映。计算情况详见下表(表6—8)。
表6—8 某项投资的标准差
| 事件i | 1 | 2 | 3 | 4 | 5 | 6 |
| 离差[γi-E(γ)] | -0. 21 | -0. 11 | 0. 01 | 0. 09 | 0. 19 | 0. 29 |
| 概率πi | 0. 15 | 0. 20 | 0. 25 | 0. 25 | 0. 10 | 0.05 |
| [γi-E(γ)]2πi | 0. 006615 | 0. 00242 | 0. 000025 | 0. 002025 | 0. 00361 | 0. 004205 |
依据表中的计算,方差为:σ2= 0.006615+0.00242+0.000025+0.002025+0.00361+0.004205=0.0189
所以标准差:
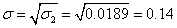
这说明该项投资的标准差为0.14。与预期报酬值相差一个标准差的实际报酬值处于1.57~1. 85(1.71±0.14)这个区域内,实际报酬落在距预期报酬值一个标准差幅度内的概率是68.26%,落在距预期报酬值两个标准差幅度以内的概率是95.45%。这样,根据标准差就可以比较不同投资风险程度的大小。例如投资于A证券和投资于B证券的预期报酬期望值相等,但A证券的标准差大于B证券的标准差,这就表明A证券的风险程度要大于B证券。
标准差Standard Devition
又称“均方差”。差异量数之一。指总体内各个变量值与其平均数之差的平方和的算术平均数,然后取算术平方根。它是用来反映变量数列的各项数值距离其中心值(或代表值)的差异程度,即离中趋势的一个指标。因为在计算差时,不计算差数的正负符号,一律取绝对值,这不符合代数的运算方法,不利于进一步对现象作统计分析。为避免采用绝对值的缺点,故用标准差这个指标来反映现象的离中趋势更为精确和恰当。标准差兼有合乎代数运算、数值稳定以及便于进一步进行统计分析等优点,是表现数列中各数值离中趋势最优良的测定指标,在数据分析中占有很重要的地位。由于标准差既具有平均差的全部优点,又适于数学运算,所以在传播研究中常与平均数相并使用,来代表个别资料的分布形态。标准差的计算在未分组的情况下,首先要求出各个变量值与其算术平均数离差的平方;然后再计算离差平方的算术平均数,公式为:
![]()
![]()
标准差
又称均方差。是各变量值与其算术平均数的离差的平方和的算术平均数的平方根,即方差的平方根为标准差。
标准差standard deviation
各变量值与其算术平均数的离差的平方和的平均数的平方根,总体标准差用σ表示。样本标准差用S或SD表示。其计算公式为: (1)对于未分组数据,式中,∑(xi-)2为各组数据离差平方和,N为数据总个数。(2)对于分组数据,式中,∑为连加符号,fi为各组的数据个数,xi为各组的中间值,为算术平均数,n为数据总个数或总频数。标准差是最重要、最常用的差异量数。用于以平均数为集中量数的场合,相互配合。它可以直接地、概括地、平均地描述变异的大小,对于同质性资料来说,标准差越小,表明数据的变异程度越小,即数据越整齐,分布范围越集中;标准差越大,表明数据的变异程度越大,即数据越参差不齐,分布范围越广。
标准差standard deviation
各变量值与其算术平均数的离差的平方的算术平均数的平方根,又称“均方差”,是统计学中最可靠、最合理、最常用的一种离中量数。样本标准差用S或SD表示,总体标准差用α表示。与平均差相比,它具有数学上易于处理的特点。平均差虽有其优点,但由于它采取绝对值的办法来消除离差的正负数,为了避免绝对值的缺陷,在统计学中就要采用标准差这一离中量数。也就是先将各项的离差数自乘,消去负号,平方以后再开平方根还原。由于各变量值与其算术平均数的差数平方之和为最小,所以标准差的计算一般皆以算术平均数为中心。同时,因标准差符合代数方法的运算,所以在统计研究中被广泛用来说明次数分配的离散趋势。标准差的计算方法:第一步,先求出各变量值与其算术平均数的离差,再把各项离差加以平方,并计算这些离差平方的算术平均数;第二步,将离差平方的算术平均数开方。从未分组材料求标准差,其公式为:
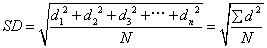
式中d1, d2, d3, …dn为一个量数系列中的每个量数与算术平均数的代数差。N为总次数。从分组材料求标准差,其计算公式为:
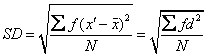
式中f为次数, 为平均数,x′为组中点,d为组中点与平均数之离差,N为总次数。
标准差standard deviation
亦称“均方差”。差异量数的一种。方差的平方根。反映一组数据的离散或相互差异程度。标准差越小,数据分布的离散程度越低,其分布的集中程度越高。平均数相同,标准差未必相同。根据数据范围,可分为样本标准差和总体标准差。现实世界中,很难获得总体数据的差异程度,一般通过样本标准差进行估计,但需要进行一定修正,才能保证估计的无偏性。
标准差
亦称“根方差”、“均方差”。方差的平方根。
- 航空法是什么意思
- 航空法是什么意思
- 航空涡轮发动机构造设计基础知识图册是什么意思
- 航空涡轮风扇发动机是什么意思
- 航空润滑油是什么意思
- 航空港是什么意思
- 航空港是什么意思
- 航空港是什么意思
- 航空火力控制原理是什么意思
- 航空火箭是什么意思
- 航空火箭弹是什么意思
- 航空炸弹是什么意思
- 航空炸弹是什么意思
- 航空热红外遥感图像集是什么意思
- 航空煤油是什么意思
- 航空燃料液态及气态下的热物理性能是什么意思
- 航空燃气涡轮发动机喷嘴制造工艺是什么意思
- 航空燃气涡轮发动机结构设计是什么意思
- 航空燃气涡轮发动机零件结构与计算是什么意思
- 航空燃气轮喷气发动机燃烧室是什么意思
- 航空燃气轮机振动和减振是什么意思
- 航空牌羽毛球是什么意思
- 航空物探是什么意思
- 航空物探解释方法及应用是什么意思
- 航空生理学是什么意思
- 航空生理学是什么意思
- 航空电器设计是什么意思
- 航空电气陀螺仪表的装配、调整和检测原理是什么意思
- 航空病是什么意思
- 航空磁测是什么意思
- 航空磁测和地面物化探找矿实例(第三集)是什么意思
- 航空移动卫星(通信)业务是什么意思
- 航空移动通信业务是什么意思
- 航空纪念日是什么意思
- 航空胶合板是什么意思
- 航空自动武器设计手册是什么意思
- 航空航天之路是什么意思
- 航空航天噪声是什么意思
- 航空航天工业部是什么意思
- 航空航天工业部第六一四研究所是什么意思
- 航空航天技术概论是什么意思
- 航空航天生理学是什么意思
- 航空装备宏观管理定量方法研究是什么意思
- 航空计费重量分界点是什么意思
- 航空调查是什么意思
- 航空货物等级费率是什么意思
- 航空货物运价手册是什么意思
- 航空货物运输是什么意思
- 航空货物运输合同实施细则是什么意思
- 航空运价是什么意思
- 航空运价是什么意思
- 航空运价是什么意思
- 航空运价是什么意思
- 航空运动是什么意思
- 航空运动是什么意思
- 航空运单是什么意思
- 航空运单是什么意思
- 航空运单是什么意思
- 航空运单是什么意思
- 航空运费是什么意思