最大似然法method of maximum likelihood

设随机变量ξ具有密度函数f (x;θ₁,θ₂，…，θ₁)，此处x为ξ的观测值，θ₁,θ₂，…，θ₁为参数。若(x₁,x₂，…，x_n)是样本(ξ₁,ξ₂，…，ξ_n)的一个观测值，那么(ξ₁,ξ₂，…，ξ_n)落在点(x₁,x₂，…，x_n)的邻域里的概率为

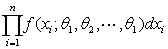
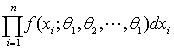最大似然法的基本思想是：样本(ξ₁,ξ₂，…，ξ_n)一次落在点(x₁,x₂，…，x_n)的邻域里的概率，一定是所有中最大的。
对回归模型Y=Xβ+u应用最大似然法时，似然函数为

此处p(Y_i)表示Y_i的概率密度，若Y_i服从正态分布，则：

为求极值方便，对似然函数求对数

解方程组

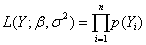
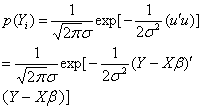
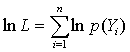
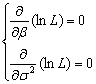
得到最大似然估计量β=(X′X)^-1X′Y,²＝e′e/n(其中e=Y-X)。
可以看出，β的最大似然估计量与最小二乘估计量完全相同，σ²的最大似然估计量略有不同，它在小样本时是有偏估计量，大样本时是一致估计量。