指数平滑法exponentialsmoothing method
又称指数修匀法。利用平滑系数对时间序列加权,求得加权平均数作为预测值的定量预测方法。它既强调时间序列中近期数据对预测值的影响,也不忽视远期数据的作用。用来加权的平滑系数呈指数几何级数形式,近期数据权数大,远期的权数小。计算公式为:
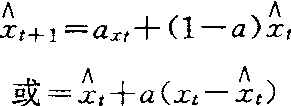
 t+1为预测值;xt为t期实际值;
t+1为预测值;xt为t期实际值; t为t期预测值;a为平滑系数,其值介于0与1之间。如时间序列的长期趋势较稳定,a应取较小的值(0.05~0.2);如时间序列有明显变动趋势,则a应取较大的值(0.3~0.5)。指数平滑法也有一次、二次、三次之分。当时间序列具有线性趋势时,用一次指数平滑法会出现较大的滞后偏差,就可再用二次指数平滑法进行趋势修正。但当时间序列数据分布出现曲率时,应采用三次指数平滑法。
t为t期预测值;a为平滑系数,其值介于0与1之间。如时间序列的长期趋势较稳定,a应取较小的值(0.05~0.2);如时间序列有明显变动趋势,则a应取较大的值(0.3~0.5)。指数平滑法也有一次、二次、三次之分。当时间序列具有线性趋势时,用一次指数平滑法会出现较大的滞后偏差,就可再用二次指数平滑法进行趋势修正。但当时间序列数据分布出现曲率时,应采用三次指数平滑法。指数平滑法
税务预测常用的一种数学预测方法。它是根据以往的实际数和预测数,通过加权平均,预测未来趋势值的一种方法。按平滑的次数不同又有一次指数平滑法和两次指数平滑法之分。税务预测较多采用一次指数平滑法。其具体作法主要分为三步:第一步确定加权系数a的值。一般根据以往的预测数和实际数的差异程度来确定,预测数和实际数差异较大,平滑系数取大一些,反之,取小一些。第二步,确定初始值。一般可以最初一期的实际数或最初若干期实际数的平均数,作为初始值。第三步,预测趋势值,即计算各期的一次指数平滑趋势值。其计算公式为:  t=aYt-1+(1-a)
t=aYt-1+(1-a)  t-1
t-1
式中 t为t期的一次指数平滑趋势值: Yt-1为最近一期的实际数值;
t为t期的一次指数平滑趋势值: Yt-1为最近一期的实际数值;  t-1为最近一期的一次指数平滑趋势值; a为平滑系数。(0≤a≤1)。指数平滑法适用于税务定量预测。
t-1为最近一期的一次指数平滑趋势值; a为平滑系数。(0≤a≤1)。指数平滑法适用于税务定量预测。
指数平滑法Exponential Smoothing
生产预测中常用的一种方法,也用于中短期经济发展趋势预测。在移动平均法基础上发展起来的一种时间序列分析预测法,即通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。
指数平滑法
亦称“指数修匀法”。根据近大远小的预测原理,建立预测模型的方法。是一个确定性时间序列预测方法,是移动平均预测法的改进。常见的有一次移动平滑法,二次移动平滑法和三次移动平滑法。
一次指数平滑预测模型是:
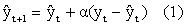
其中体现的预测思想是,一个新的预测值等于前期旧的预测值再加上一个前期预测误差调整项。(1)式中,α为平滑系数,yt为时间序列 {yt} 的第t期观察值,
 是其预测值。把(1)式递推展开,就可以得到:
是其预测值。把(1)式递推展开,就可以得到: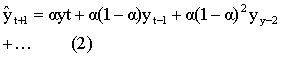
 t+1,实际上是第t期的指数平滑值。 (2)式右边的权系数是指数几何级数,指数平滑也由此得名。一次指数平滑法用于实际数据序列以随机变动为主、没有明显变动倾向的场合。其优点是:
t+1,实际上是第t期的指数平滑值。 (2)式右边的权系数是指数几何级数,指数平滑也由此得名。一次指数平滑法用于实际数据序列以随机变动为主、没有明显变动倾向的场合。其优点是:❶对不同时间的数据的非等权处理较符合实际;
❷仅选定一个参数α即可预测,简便易行;
❸具有适应性,即预测模型能自动识别数据模式的变化而加以调整。
二次指数平滑法,就是对一次指数平滑值序列再作一次指数平滑,并在此基础上,仿照二次移动平均法,根据滞后偏差的演变规律来建立线性预测模型,适用有线性增长倾向的情形。
三次指数平滑法,是对二次指数平滑值序列再作一次指数平滑,并在此基础上建立非线性预测模型,适用于实际数据序列有非线性增长倾向的情形。
指数平滑法exponential smoothing method
亦称“指数修匀法”。根据近大远小的预测原理,建立预测模型的方法。是一个确定性时间序列预测方法,是移动平均预测法的改进。常见的有一次移动平滑法,二次移动平滑法和三次移动平滑法。
一次指数平滑预测模型是:
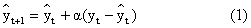
其中体现的预测思想是,一个新的预测值等于前期旧的预测值再加上一个前期预测误差调整项。(1)式中,α为平滑系数,yt为时间序列{yt}的第t期观察值,
 t是其预测值。把(1)式递推展开,就可以得到:
t是其预测值。把(1)式递推展开,就可以得到: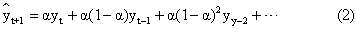
 t+1,实际上是第t期的指数平滑值。 (2)式右边的权系数是指数几何级数,指数平滑也由此得名。一次指数平滑法用于实际数据序列以随机变动为主、没有明显变动倾向的场合。其优点是:
t+1,实际上是第t期的指数平滑值。 (2)式右边的权系数是指数几何级数,指数平滑也由此得名。一次指数平滑法用于实际数据序列以随机变动为主、没有明显变动倾向的场合。其优点是:❶对不同时间的数据的非等权处理较符合实际;
❷仅选定一个参数α即可预测,简便易行;
❸具有适应性,即预测模型能自动识别数据模式的变化而加以调整。
二次指数平滑法,就是对一次指数平滑值序列再作一次指数平滑,并在此基础上,仿照二次移动平均法,根据滞后偏差的演变规律来建立线性预测模型,适用有线性增长倾向的情形。
三次指数平滑法,是对二次指数平滑值序列再作一次指数平滑,并在此基础上建立非线性预测模型,适用于实际数据序列有非线性增长倾向的情形。
指数平滑法Exponential Smoothing Method
时间数列分析预测技术的一种方法。这种方法是美国人布朗于1959年首次提出的。指数平滑法在进行预测时,只涉及两个资料:本期实际值和本期预测值。它实际上是一种移动平均法的变形。以Rt代表本期实际值,St代表本期预测值,St+1代表下期预测值,指数平滑公式可表示为:St+1=St+a(Rt-St)=aRt+(1-a)St,其中a即为平滑系数,它的取值介于0和1之间。a的具体取值一般应根据数据的实际情况,经过试算,选取若干个不同值,经过比较后取预测误差最小的值作为一次指数平滑系数。若短期的情况对预期发生作用较大时,a取值也应权重大些。作为一种时间数列分析方法,指数平滑法对于变动不规则的时间数列进行修匀和预测是比较有效的。
指数平滑法
利用上期预测值和上期实际值资料,以平滑系数α为加权因子,计算出指数平滑平均数来作为本期预测值的方法。因为此法只要有上期预测数和上期实际数两个数据,就可进行预测,计算简便,所以应用较广泛。此法为美国布朗所创。其计算公式如下:
 t+1=
t+1= t+α(Yt-
t+α(Yt- t)=αYt+ (1-α)
t)=αYt+ (1-α) t
t
 t+1=5.54+0.2(6.45-5.54)=5.722
t+1=5.54+0.2(6.45-5.54)=5.722
指数平滑法exponential smoothing
用于预测的平滑法中的一种,在这里,对一个时期(t+1期)的预测值是前期(t期)时间序列的实际值与预测值的加权平均数。
平滑法是一种粗线条的预测方法。它仅以其过去值的某种平均数为依据来预测一个时间序列的未来值。最简单的平滑法是移动平均法,在这里,一个时间序列在指定时期内的预测值等于该时间序列在以前若干时间内的平均值。此法的严重缺陷是,它在计算平均值时对所有观察值皆给以相等的权数,即使我们可以直观地认为最近期的观察一般说应是更为重要的。为克服这一缺陷,人们在预测中更经常地使用指数平滑法。
指数平滑法的公式如下:Ft+1=ωA1+(1-ω)Ft,式中Ft+1为(t+1)期的预测值,At为t期内时间序列数值(实际值),Ft为t期的预测值;ω为权数,ω的值在0—1之间。显然,ω的值越大,则给t期的时间序列数值(相对于以前的各期而言)的权数越大。
使用此法,须作两个决定:一是确定Ft之值。这种做法是令Ft等于全部时间序列观察值的均值。二是确定ω之值。通常,对ω可试以不同之值,而用平方根误差(RMSE)最小的一个。
指数平滑法
时间序列预测方法之一。根据时间序列的指数平滑平均数来进行预测的一种方法。指数平滑平均数的计算公式为:
St(1)=αyt+(1-α) St-1(1)。
式中,Si(1)代表第i期一阶指数平滑平均数; yt代表基期的时间序列值; α代表平滑系数,通常依经验确定。同理,还可计算二阶、三阶指数平滑平均数:
St(2)=αSt(1)+(1-α)St-1(2);St(3)=αSt(2)+(1-α)St-1(3)
指数平滑法主要包括: (1) 一次指数平滑法。直接以本期的一阶指数平滑平均数作为下期的预测值的方法。预测模式为:
yt+1 =St(1)= αyt+ (1-α)  t.即下期的预测值等于本期的时间序列值与本期的预测值的加权平均数。主要用于时间序列在某一范围内波动,但无上升、下降趋势时的短期预测。(2) 二次指数平滑法。根据一阶和二阶指数平滑平均数来进行预测。预测模式为: yt+k =at+kbt。其中,参数at、bt可由一阶、二阶指数平滑平均数求得:
t.即下期的预测值等于本期的时间序列值与本期的预测值的加权平均数。主要用于时间序列在某一范围内波动,但无上升、下降趋势时的短期预测。(2) 二次指数平滑法。根据一阶和二阶指数平滑平均数来进行预测。预测模式为: yt+k =at+kbt。其中,参数at、bt可由一阶、二阶指数平滑平均数求得:
at=2St(1)-St(2);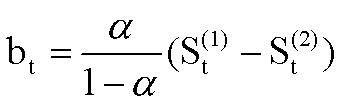
主要用于时间序列呈明显的线性上升、下降趋势时的预测,既可作短期预测,也可作中、长期预测。(3) 三次指数平滑法。根据一阶、二阶和三阶指数平滑平均数来进行预测。预测模式为: yt+k=at+btk+ctk2。其中,参数at、bt、ct可依一阶、二阶、三阶指数平滑平均数求得:
at=3St(1)-3St(2)+St(3);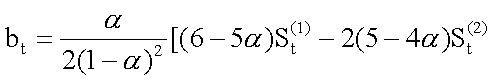 +(4-3α) St(3)];
+(4-3α) St(3)];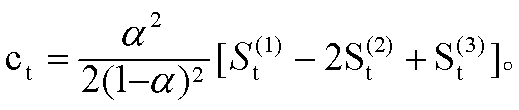 可以用于时间序列出现非线性趋势时的各种情况的预测。
可以用于时间序列出现非线性趋势时的各种情况的预测。
- 无限责任公司是什么意思
- 无限量发售申请表方式是什么意思
- 无限防卫是什么意思
- 无限风光在险峰是什么意思
- 无限风光在险峰是什么意思
- 无隙内接头是什么意思
- 无隙可乘是什么意思
- 无隙可乘是什么意思
- 无隙可乘是什么意思
- 无隙可乘是什么意思
- 无障碍最低标准是什么意思
- 无障碍物区是什么意思
- 无障碍环境设计是什么意思
- 无震海岭是什么意思
- 无靠无依是什么意思
- 无面值股票是什么意思
- 无面值邮票是什么意思
- 无面目见江东父老是什么意思
- 无面目见江东父老是什么意思
- 无面额股票是什么意思
- 无音是什么意思
- 无音是什么意思
- 无音是什么意思
- 无音是什么意思
- 无韵诗是什么意思
- 无韵诗和散文诗的提倡是什么意思
- 无须误死是什么意思
- 无须鳕是什么意思
- 无领导小组讨论是什么意思
- 无题是什么意思
- 无题是什么意思
- 无题是什么意思
- 无颠无倒是什么意思
- 无风不起浪是什么意思
- 无风不起浪是什么意思
- 无风才到地,有风还满空。缘渠偏似雪,莫近鬓毛生是什么意思
- 无风起浪是什么意思
- 无风起浪是什么意思
- 无风起浪是什么意思
- 无风起浪是什么意思
- 无风起浪是什么意思
- 无食子是什么意思
- 无食子丸是什么意思
- 无食子丸是什么意思
- 无食子丸是什么意思
- 无食子散是什么意思
- 无验于事者,其言不合是什么意思
- 无验而言之谓妄是什么意思
- 无髓纤维是什么意思
- 无髓纤维是什么意思
- 无鬼论是什么意思
- 无鱼不成席是什么意思
- 无齿邮票是什么意思
- 无,名天地之始是什么意思
- 既是什么意思
- 既是什么意思
- 既是什么意思
- 既是什么意思
- 既是什么意思
- 既是什么意思