布尔代数buerdaishu

研究逻辑电路（也叫开关电路）的一种数学工具，如同普通数学中的代数一样，也有变量和常量，研究方法也类似，所以叫逻辑代数，是英国数学家乔治·布尔发明的，故常称布尔代数.
逻辑常量只有0和1两个数值，逻辑变量可用字母表示.布尔代数有三种最基本的逻辑运算：
❶逻辑加(亦叫逻辑或，“或”)
0+0=0 这个“+”号，表示逻辑加
0+1=1+0=1
1+1=1.

❷逻辑乘(亦叫逻辑与，“与”)
0·0=0 这个“·”号，表示逻辑乘
0·1= 1.0=0
1·1=1

❸逻辑非（亦叫求反运算）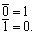

布尔代数在逻辑电路设计中很有用，在设计中先根据电路要求的输入和输出对应关系，列出真值表，再列出逻辑表达式，然后利用布尔代数的基本公式进行化简（也可用卡诺图进行化简），最后得到最简单的逻辑电路.

---

布尔代数buer daishu

有补分配格.布尔(1815—1864)在研究命题演算时，发现命题代数与集合代数具有许多相同的算律：交换律、结合律、分配律、幂等律、吸收律、德·摩根律等.从代数学观点，必然要问，能否研究一种抽象的代数系统，同时具有命题代数与集合代数所具有的最本质的性质？布尔于1854年提出了布尔代数的概念.
集合代数〈P (S),∪,∩,Φ,S〉，当|S|有限时，是有限布尔代数，含2ⁿ个元，|S|=n.并且，可以证明，任何含2ⁿ个元的有限布尔代数都与〈P(S),∪,∩,Φ,S〉同构，因而亦彼此同构.命题代数是无限的布尔代数.

布尔代数

即“逻辑代数”。

---

布尔代数

又称“逻辑代数”。设B是一个至少有两个元素的集合，其中定义了两种运算：+（加法）,*（乘法）,B中元素对于这两种运算，如果满足以下公理：对任意x、y、z∈B,(ⅰ):x+y=y+x,x*y=y*x;(ⅱ):x*(y+z)=(x*y)+(x*y);x+(y*z)=(x+y)*(x+z)(ⅲ):B中有元素0和1满足：x+0=x,x*1=x*(iv):对任意x∈B，有x∈B，使x+x¹＝1,x*x′=0，则称B为一个布尔代数。如：令B={0,1}，定义：

该系统即为 一布尔代数。

布尔代数

又称“逻辑代数”，是英国数学家、逻辑学家布尔(George Boole)1815—1864所创立的一个代数系统。布尔认为，逻辑关系和某些数学运算甚为类似，代数系统可以有不同的解释，把解释推广到逻辑领域，就可以构成一种思维的演算。他在其著作《逻辑的数学分析》(1847年)及《思维规律》(1854年)中引进了逻辑代数的基本概念，构成了一个抽象代数系统。用这种系统可以较容易地处理传统逻辑所不能处理的逻辑问题。布尔对他的代数系统给出了四种解释：一种是类的演算，两种是命题的演算，一种是概率演算。
经过后来数学家的进一步改进，布尔代数成为如下的一个数学系统：设B是一个至少有两个元素的集合，其中定义两种运算：+ （逻辑加法）, *（逻辑乘法）,B中元素对于这两种运算，如果满足下面公理：对任意的x,y,z∈B。
公理1:x+y=y+x; x*y=y * x;
公理2: x * (y+z)=(x * y) + (x * z);
x+ (y * z)=(x+y) * (x+z);
公理3: B中有元素0和1满足：
x+0=x;x *1=x;
公理4:对任意x∈B，有x′∈B，使
x+x′ =1;x * x′ =0;
则称B为一个布尔代数。
例如，令B={0,1}，让1表示真命题，0表示假命题，定义+运算如下：
0+0=0;0+1=1;1+0=1;1+1=1;
定义*运算如下
0 * 0=0;0 * 1=0;1 * 0=0;1 * 1=1;
则它表示的就是一个命题代数的系统。由于有1+1=1，它不同于一般的代数系统。
在布尔代数的基础上，人们又发展了开关代数。
开关代数在组合电路、电路网络中有极大的应用价值。