套利价格理论

确定资产均衡价格，即确定期望证券报酬和风险的理论。由美国经济学家S·罗斯建立。
假设前提：
❶投资者具有相同的预期；
❷投资者是风险反对者和最大效用追求者；
❸市场是完善的，从而没有交易费用等不完善性；
❹投资者具有相同的单一持有期；
❺没有税收；
❻投资者可以自由地以无风险利率借入和借出；
❼投资者在期望报酬和报酬方差的基础上选择投资组合。
因素模型和因素投资组合。罗斯认为，在整个经济中存在着一些主要的和具有普遍影响的市场因素，它们在不同程度上影响着许多公司和各种证券的报酬，因此，对于某种证券来说，其报酬是不确定的，它由三个部分构成：
❶没有这些市场因素时的期望报酬，即“无因素关联”报酬；
❷由这些市场因素产生的报酬，对于每一种因素来说，其对某种证券所产生的报酬等于此因素报酬的期望值乘以该证券的报酬对此因素变动的敏感系数；
❸证券个别风险的报酬。这样，如果只存在一个市场因素时，证券i的报酬可以表示如下：

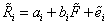
式中_i代表证券i的不确定报酬；a_i代表无因素关联报酬；b_i代表证券i的报酬对市场因素的敏感系数；代表因素的不确定报酬值；_i代表不确定的证券个别报酬。一般地，对一个包含有N个市场因素的情况，证券i的报酬表示为：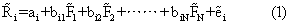

上式即为因素模型的一般形式，它隐含着三个假定：
❶证券个别报酬的期望值为0;
❷证券个别报酬与各因素无关联；
❸证券个别报酬间无相互关联。假定这N个市场因素已经被确定，与他们相关的证券报酬由(1)式给出（包括其三个隐含的假定），还假定存在着许多证券且证券之间对这些因素的敏感程度大不相同。这样，就能建立一个纯因素投资组合，即该投资组合只对某一因素敏感而不受其他因素影响，并且高度多样化从而使证券个别报酬为0。
纯因素投资组合的期望报酬和证券期望报酬。一个纯因素投资组合的期望报酬，依赖于该有关因素的期望值，该投资组合的期望报酬分为两个部分：
❶无风险利率R_f
❷期望报酬与无风险利率间的差额λ，它可以认为是每单位对纯因素的敏感度所引起的期望报酬的溢价。因此，纯因素之投资组合的期望报酬可表示为R_f+λ_i。
假定证券i对因素1和2敏感，其报酬为：

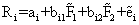
某投资者现有投资1美元，又借入无风险证券(b_i1+b_i2-1)美元，使投资总额达(b_i1+b_i2)美元。该投资者将b_i1美元投资于因素1投资组合，把b_i2美元投资于因素2投资组合，这样组成了投资组合i的期望报酬E_i:
若 无风险利率为-(b_i1+b_i2-1)R_f=-b_i1R_f—b_i2R_f+R_f
因素1 投资组合为b_i1(R_f-λ₁)=b_i1R_f+b_i1λ₁
因素2 投资组合为b_i2(R_f+λ₂)=b_i2R_f+b_i2λ₂
则E_i=-(bi₁+b_i2-1)R_f+b_i1(R_f+λ₁)+b_i2(R_f+λ₂)R_f+b_i1λ₁+b_i2λ₂
把证券i的报酬与投资组合i的期望报酬进行比较，可以发现，两者对因素1的敏感系数均为b_i1，对因素2的敏感系数均为b_i2，证券之遭受其证券个别风险，而投资组合i则没有。如果证券i的期望报酬低于投资组合i的期望报酬，那么套利者就会卖空证券i，用此收益来购买投资组合i，希望从两者报酬的差异中获利，反之亦然。当然，这个买卖过程并非完全无风险，因为证券个别报酬可能淹没两者报酬的差异。但是，如果有大量的i那样的证券，则这种证券个别风险可以被多样化消除。因此套利使证券i的期望报酬非常近似于：

E_k=R_f+b_i1λ₁+b_i2λ₂

如果有N个市场因素，则：

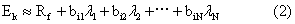
上式揭示了套利价格理论的结论：证券和投资组合的期望报酬与其对市场因素的敏感度相关，而且这个关系是线性的。报酬的起点为无风险利率。
证券和投资组合的β值。根据协方差的性质，可推导出证券i相对于市场组合的β值，从而得出结论：某种证券或投资组合的β值是各有关因素的β值的加权平均数，权重为该证券或投资组合对各因素的敏感度。
套利价格理论以证券更受市场中具有普遍影响因素的影响为出发点，运用相同的投资组合应提供相同的报酬（以防止套利）这一经济原理，推导了影响证券报酬的各种因素的市场价格。证券的均衡报酬，于是就与它们对各种因素的敏感度和各种因素的市场价格相联系。