四元术

 四元术是元代著名数学家朱世杰的一项数学成就，记载于他的数学著作《四元玉鉴》之中，祖颐在为《四元玉鉴》写的序文中记录了朱世杰的数学思想，其中“用假象真，以虚问实”这在我国数学著作中还是第一次出现。四元术是用四元消法解题。天元、地元、人元、物元代表四个未知数，它各为一次、二次直至四次方，甚至可以发展为高次方。它把四元四式消去一元，变成三元三式，再消去一元，变成二元二式，就得到了一个只含一元的天元开方式。然后用增乘开法求得正根。这与解方程组的方法基本一致。直到18世纪法国数学家别朱于1775年才系统地叙述了高次方程组的消元方法。

079 四元术

建立和求解多元高次方程组的方法。朱世杰的主要数学成就之一。早在公元一世纪，《九章算术》已给出了建立和求解多元一次方程组的方法。其后久无显著进展。贾宪、秦九韶、李冶等人潜心于天元术(布列一元高次方程的方法)的研究，使之日臻完善。13世纪中叶，河北、山西一带的数学家对多元高次方程始有提及。李德载引入二元高次方程组，刘大鉴提出二元高次方程组二例。在此基础上，朱世杰集前贤之大成，在《四元玉鉴》中建立了四元高次方程组的理论。他用天、地、人、物代表未知数，然后根据已知条件用等式列出四元(或二元三元)方程组。实际上是多元高次方程组。这是中国古代位值制记数法的又一新发展。解此方程组，需对四元等式进行变换，逐次消元，化为一个关于某一未知数的一元高次方程，然后用增乘开方法求其正根。以二元二次方程组为例，假设方程组已整理为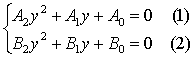

其中A_i、B_i(i=0,1,2)均表示关于x(不含y)的多项式，以B₀乘(1)、A₀乘(2)，相消得C₁y+C₀＝0(3)再由(1)、(3)或(2)、(3)相消得D₁y+D₀＝0(4)由(3)、(4)相消得一元方程。此即朱世杰的消元法。对于高于2次或三元、四元方程组，此法均适用。这是世界上最早的多元高次方程组解法。它已和今天解多元高次方程组的方法基本相同。其整个变换过程也是世界数学史上最早出现的多项式运算。 1764年，法国数学家贝祖(.Bézout,1730—1783)在《代数方程的一般理论》中提出了高次方程组的消去法，迟于朱世杰近500年。

四元术

中国古代建立四元高次方程组的方法和解法。中国最初以天元表示一个未知量，13世纪朱世杰在《四元玉鉴》中用天、地、人、物四元表示4个未知量，并举例说明建立四元高次方程组及消元的方法。