命题逻辑

数理逻辑的基础部分，研究以原子命题为基本单位，由真值联结词所构成的复合命题的逻辑特征及其规律的逻辑演算理论。

命题逻辑

亦称命题演算。指处理复合命题及其逻辑关系，并将所有的重言式组成一个完全形式化的符号系统。与谓词逻辑不同，命题逻辑在研究和考查逻辑形式时，将一个命题只分析到其中所含的命题成分为止，而不再把一个简单命题再分析为非命题成分例如个体词、量词、谓词的结合。它用命题变元例如p、q、r、s等表示不确定的任意一个命题，使用了五个命题联结词：合取(用“∧”表示)、析取(用“∨”表示)、蕴涵(用“→”或“⊃”表示)、等值(用“←→”表示)、否定(用“乛”表示)，按照下面的形成规则把命题变元联结成复合命题表达式。这种表达式经过解释是有意义的句子，称为良构式。
形成规则
（一）任一命题变元是一良构式。
（二）如X是良构式，则乛X是良构式。
（三）如X和Y是良构式，则X∧Y、X∨Y、 X→Y、X←→Y是良构式。
（四）只有适合以上三条的符号序列是良构式。这样就可以把没有意义的表达式如p∧∨q,p→,p←→qr等排除在系统之外。
命题逻辑不仅使用了特有的表意符号语言，而且通常构成一个公理系统。系统不同，作为推导的出发点的公理也不完全相同。下面是两个最常见的系统的公理，第一个是经过改造的弗雷格公理系统，第二个是罗素公理系统。

弗雷格系统的公理

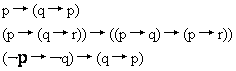
罗素系统的公理

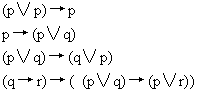
为了从公理出发，逻辑地推导出其它的定理，命题逻辑制定了变形规则。变形规则主要有两条：
（一）代入规则。对公理及推导出来的定理中某一命题变元处处代以某一良构式，则代入后的表达式也是定理。
（二）分离规则。从推出A和A→B，可推出B。
从公理出发，依据变形规则，命题逻辑可以进行一系列的推导。推导的过程纯粹是符号序列的变形，而不涉及符号的任何意义。推导出来的定理都反映了逻辑的规律，都表现为重言式。
对于一个命题逻辑的公理系统，还需要考查它是否满足一致性的要求。一致性也就是无矛盾性，它是对一个系统的根本要求，因为如果一个系统里存在着逻辑矛盾，A和非A都在这个系统里可证，那么这个系统就是不正确的。通过证明，命题演算的公理都是重言式，并且应用命题演算的变形规则，从重言式只能得到重言式，因此，命题演算公理系统是一致的。
重言式的数量是无穷无尽的。命题演算公理系统从公理和变形规则出发，能否把所有的重言式无一遗漏地推演出来，这是系统的完全性问题。有两种方法可以证明命题演算的完全性。其一是通过和重言式对应的合取范式是可证的，表明凡重言式在系统内都是可证的。其二是当添加一不可证的公式作为公理时，命题演算就不再具有一致性。
对于一个公理系统，还要求它的公理最好具有独立性，即其中的任何一条公理，都不能通过其余的公理应用变形规则推演出来。通常采用算术解释方法来达到这一点：赋于变项和公式以数值，其余的公理只能得某个数值，它们应用变形规则也只能得这个数值，而要证明其独立性的公理在这种赋值下却能得到另外一个不同的数值。用这种方法可以证明上面介绍的两组公理都满足独立性的要求。
对于任意一个表达式，命题逻辑有一能行的程序判定其是否重言式，是否在系统中可证。方法是先求出任一表达式A的合取范式B。如B不是重言式，则B不是定理，因而A也不是定理，不可证。如B是重言式，则求证B。求证一合取范式是否重言式，可以完全机械地进行。因此，命题逻辑是可判定的。
命题逻辑是其他的演绎逻辑如谓词逻辑、模态逻辑等的基础。

命题逻辑

propositional logic