合数术
十一卷。英白尔尼撰,傅兰雅(详见《数学理》)、华衡芳 (详见 《代数术》) 合译。《合数术》 译本无原著写作年代。作者在 “总引” 中指出:“此书所论之理,谓之合数,乃算学中一种新术,并非将旧术所能推之事,更立新法也。”“西国始悟得此术之人,名曰密几理。自密几理以前,未有人考究此种数理也。”“此种算学能推广真数之作用,扩充算学之界限,又能设立新法,使甚难而大有用之题易推,可免用表及其繁之式,并不足凭之略法。”“此书中所有之算式,并非删繁就简,每算一题,必将其层累曲折,步步写出,因不欲之致迷也。”这是一部介绍合数算法的专著,它的造算过程繁复冗长,并需依靠“合数表”。其内容如下:卷首总引中先介绍“合数术”总貌,尔后在“卷首(上)”讲述合数的定义、记号,合数与常数的互换方法。在“卷首(下)”中给出六种互换表,并取大量例题以明其用。卷一一卷三论述合数的基本运算:乘法、除法、乘方及开方法。卷四一卷六讨论合数在平面三角、球面三角中的应用。卷七一卷九论述用合数之法解各种代数方程。其中较有特色的是解方程 x2—120x—100x1/2+999x1/3=91000,求得x=358.98937。还有解方程xx=8722.83528,求得x=5.38776485. 卷十为“杂题之法”。其内容有代数、方程、三角测量、椭圆积分、球面三角以及一些较深的物理问题。卷十一再论“合数开方术”,即代数方程求根的问题。并称“代数学之功夫大半从相等内求出其未知之数,……,从前最有名之各算家已费尽大力欲求各次乘方式之根,迄未能得公法,固惟用数学以求各方之根,其法最为繁重。”认为“此书所设之公法不难合于平常各事之用,故可以云:此法为代数学内所增之各门中最益之事,无此公法,则代数之学未为完善也。”在卷首 (上) 中给出的 “合数”定义是:“凡数无论何数,命之为 (N),皆能化之为级数连乘之形”即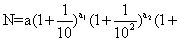
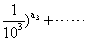 省去括号内的底数,仅以指数记之为:N=a↓a1,a2,a3,……,其中ai(i=1,2,…)即是N的合数。一般说来,这种化实数为合数的结果不唯一,即一个实数的合数形式有多种。原著以π为例说明之: 即3.1415927=↓12,0,1,0,0,8,2,3=↓12,0,0,10,0,6,16,18=↓10,15,40,20,35,40,30,25=↓7,42,56,35,14,28,49,7=↓0,0,0,0,0,0,0,114478742。据合数定义,合数的乘除之法为: α↓α1,α2,αn×β↓β1,β2,…,βn=α·β↓ α1+β1,α2+β2,…,αn+βn. α↓α1,α2,…,αn÷β↓β1,β2,…,βn=α/β=α/β↓α1-β1,α2-β2,…,αn-βn。书中还以大量篇幅讨论合数与常数的互化问题。为了阐明合数的应用,原著举了大量例子,涉及到西方近代科学领域,这对于研究西方科学的传入颇为重要。其中有:卷七第十题“解代数各次相等之式公法”给出了正态分布函数和曲线;卷十“用合数解数种紧要之题”第十四题以汽缸活塞运动为对象讨论了平衡过程的做功; 第十五题“摆以平圆线摆动之时”,讨论了单摆问题。通过介绍可知《合数术》立术新颖,应用较广,并非专论对数。不过由于其计算过于繁复冗杂不易掌握,终未成气候而逐渐消亡。傅、华两氏的《合数术》十一卷译本,终未能刊刻,但晚清学者林绍清于1888年刻印出版了《合数述》二卷,是《合数术》的节本。后人对《合数术》的研究因资料所限而未能进行。当代中算史家李迪于五十年代在上海书坊购得《合数术》五册十一卷,扉页上书:“此册为余手写校定之本,依此写校,即可付梓矣。蘅芳识。”可见这是华氏稿本,现藏李迪处。李迪的研究生纪志刚在《稿本〈合数术〉研究》(载《数学史研究文集第一辑》)中对此稿本作了详细介绍和初步研究。
省去括号内的底数,仅以指数记之为:N=a↓a1,a2,a3,……,其中ai(i=1,2,…)即是N的合数。一般说来,这种化实数为合数的结果不唯一,即一个实数的合数形式有多种。原著以π为例说明之: 即3.1415927=↓12,0,1,0,0,8,2,3=↓12,0,0,10,0,6,16,18=↓10,15,40,20,35,40,30,25=↓7,42,56,35,14,28,49,7=↓0,0,0,0,0,0,0,114478742。据合数定义,合数的乘除之法为: α↓α1,α2,αn×β↓β1,β2,…,βn=α·β↓ α1+β1,α2+β2,…,αn+βn. α↓α1,α2,…,αn÷β↓β1,β2,…,βn=α/β=α/β↓α1-β1,α2-β2,…,αn-βn。书中还以大量篇幅讨论合数与常数的互化问题。为了阐明合数的应用,原著举了大量例子,涉及到西方近代科学领域,这对于研究西方科学的传入颇为重要。其中有:卷七第十题“解代数各次相等之式公法”给出了正态分布函数和曲线;卷十“用合数解数种紧要之题”第十四题以汽缸活塞运动为对象讨论了平衡过程的做功; 第十五题“摆以平圆线摆动之时”,讨论了单摆问题。通过介绍可知《合数术》立术新颖,应用较广,并非专论对数。不过由于其计算过于繁复冗杂不易掌握,终未成气候而逐渐消亡。傅、华两氏的《合数术》十一卷译本,终未能刊刻,但晚清学者林绍清于1888年刻印出版了《合数述》二卷,是《合数术》的节本。后人对《合数术》的研究因资料所限而未能进行。当代中算史家李迪于五十年代在上海书坊购得《合数术》五册十一卷,扉页上书:“此册为余手写校定之本,依此写校,即可付梓矣。蘅芳识。”可见这是华氏稿本,现藏李迪处。李迪的研究生纪志刚在《稿本〈合数术〉研究》(载《数学史研究文集第一辑》)中对此稿本作了详细介绍和初步研究。
- 脉诀规正是什么意思
- 脉诀辨明 明 徐枢是什么意思
- 脉诀辨疑 明 施世杰是什么意思
- 脉诀辨讹 清 徐大楫是什么意思
- 脉诀辨误 清 余韹是什么意思
- 脉诀集解是什么意思
- 脉证合参是什么意思
- 脉证合参是什么意思
- 脉证合参是什么意思
- 脉证合参是什么意思
- 脉证类议 明 鲍叔鼎是什么意思
- 脉证要诀是什么意思
- 脉诊是什么意思
- 脉诊是什么意思
- 脉诊是什么意思
- 脉诊是什么意思
- 脉诊是什么意思
- 脉诊是什么意思
- 脉诊便读是什么意思
- 脉诊便读是什么意思
- 脉诊八段锦是什么意思
- 脉语是什么意思
- 脉语是什么意思
- 脉说是什么意思
- 脉说是什么意思
- 脉说是什么意思
- 脉谱 清 张园真是什么意思
- 脉象是什么意思
- 脉象是什么意思
- 脉象是什么意思
- 脉象主病是什么意思
- 脉象图与脉诊客观化是什么意思
- 脉象统类是什么意思
- 脉象辨真 清 张永和是什么意思
- 脉贯是什么意思
- 脉赋训解是什么意思
- 脉逆四时是什么意思
- 脊是什么意思
- 脊三是什么意思
- 脊中是什么意思
- 脊令是什么意思
- 脊令原是什么意思
- 脊令在原是什么意思
- 脊尾白虾是什么意思
- 脊强是什么意思
- 脊强是什么意思
- 脊柱是什么意思
- 脊柱是什么意思
- 脊柱前凸是什么意思
- 脊柱外科学是什么意思
- 脊柱裂是什么意思
- 脊柱裂伴脊髓脑脊膜膨出是什么意思
- 脊柱骨折与脱位是什么意思
- 脊梁是什么意思
- 脊梁颂是什么意思
- 脊椎动物是什么意思
- 脊椎动物是什么意思
- 脊椎动物分类学是什么意思
- 脊椎动物多倍体是什么意思
- 脊椎动物学是什么意思