可积函数类keji hanshulei

❶若函数f (x)在区间 [a,b]上连续，则f (x)在区间 [a,b]上可积。

❷若函数f (x )在区间 [a,b]上有界，且只有有限个间断点，则f (x)在区间 [a,b]上可积。

❸若函数f (x)在区间 [a,b]上单调，则f (x)在区间 [ a,b ] 上可积。
上述定理给出了函数可积的充分条件，换言之，上述三类函数具有在闭区间上可积这种性质，在这三类函数之外，也还存在可积函数. 如函数

f (x)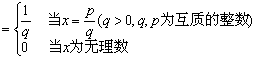

在区间 [0,1]上可积，但不属于上述的任何一类函数。
证明这三个定理，要用到实数域的连续性和闭区间上连续函数的性质。