t—分布

---

也称“学生氏分布”。

在推断平均数时一般都要用到总体方差，而多数情况下总体方差系未知数，须用样本方差代替，这就会导入一定误差，若抽样数目不大(小样本)，误差则会影响到必要的精确度。因而必须在计算公式中避免运用总体方差来克服这个缺点。为此，英国酿酒专家、统计学家科萨得以Student(学生)为笔名提出著名的t－分布，故也称学生氏分布。设X服从正态分布N(0，1)，y服从x²－分布X²(n)，且x与y相互独立，则随机变量：

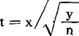
服从自由度为n的t－分布，记作t～t(n)，其概率密度函数为：

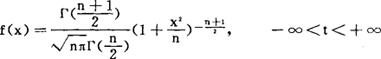
t－分布为对称分布，形似正态分布，但t－分布曲线两端较正态分布曲线为凸起。

以t=0对称。当n很大时，t分布近似于正态分布n(0，1)，故通常t分布表只列出自由度由1～30，若自由度大于30，则可应用正态分布。

t－分布的应用范围广泛，主要可用作：总体平均数的估计；样本与总体间平均数显著性检验；两个样本平均数差异的显著性检验；平均量差异的估计。