勾股定理

 故折矩以为勾广三，股修四，径隅五。既方之外，半其一矩，环而共盘，得成三、四、五。两矩共长二十有五，是谓积矩。
 

汉《周髀算经》卷上

 若求邪至日者，以日下为勾，日高为股。勾、股各自乘，并而开方除之，得邪至日。
 

汉《周髀算经》卷下

 【评】这是《周髀算经》中有关勾股定理的记载。前者据传是
 周公与商高问答的内容，只是一个特例，尚不能称为勾股定理；后者出自陈子答荣方问，已有勾股定理的较为抽象的形式。
 勾股术曰：勾、股各自乘，并，而开方除之，即弦。
 又，股自乘，以减弦自乘，其馀，开方除之，即勾。
 又，勾自乘，以减弦自乘，其馀，开方除之，即股。
 

汉《九章算术·勾股》

 【评】此为勾股定理在中国第一次完整的抽象表述：,其中a,b,c分别为勾、股、弦。西方称之为毕达哥拉斯定理，是中国古代数学一重要分支——勾股理论的基础。
 勾股之法，先知二数，然后推一。见勾、股，然后求弦，先各自乘，成其实。实成势化，尔乃变通，故曰：“既方其外”。或并勾、股之实以求弦。弦实之中乃求勾、股之分并。实不正等，更相取与，互有所得。故曰“半其一矩”。
 

《周髀算经》赵爽注

 【评】此为赵爽对商高勾三股四弦五的注，阐明了勾股定理的一般形式。
 短面曰勾，长面曰股，相与结角曰弦。勾短其股，股短其弦。将以施于诸率，故先具此术以见其源也。
 

《九章算术·勾股》三国魏·刘徽注

 【评】此为刘徽对勾、股、弦的界说，并阐明了勾股定理对勾股理论的意义。
 勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其馀不动也，合成弦方之幂。开方除之，即弦也。
 

《九章算术·勾股》三国魏·刘徽注

 然二幂之数谓倒在于弦幂之中而已，可更相表里，居[原本脱“表里居”三字，李潢补]里者则成方幂，其居表者则成矩幂。二表里形讹而数均。又按：此图，勾幂之矩青，卷白表，是其幂以股弦差为广，股弦并为袤，而股幂方其里。股幂之矩青，卷白表，是其幂以勾弦差为广，勾弦并为袤，而勾幂方其里。是故差之与并用除之，短长互相乘也。
 

《九章算术·勾股》三国魏·刘徽注

 【评】此两条，前者为刘徽用出入相补原理对勾股定理证明的提示；后者指出勾(股)方与股(勾)矩合成弦方，在解勾股形中用处极大。

勾股定理

几何定理。内容为：在直角三角形中，斜边的平方等于两条直角边的平方的和。这个定理，西方称为毕达哥拉斯定理，据认为是毕达哥拉斯(公元前572～前497)首先给出了这个定理的证明。在中国古代，大约成书于公元前235年至公元前145年之间的《周髀算经》中，就有“故折矩以为句（勾）广三、股修四、径隅五”，“句（勾）股各自乘，并而开方除之，得邪至日”的记载，前者是定理的特例，后者则是定理的一般形式。三国时期的数学家赵爽给出了证明。此定理在中国发现的年代不可考，但无可怀疑地应在《周髀算经》成书之前。

016 勾股定理

中国传统数学中一个基本而又十分重要的定理。其内容为：在直角三角形中，斜边的平方等于两直角边的平方和。中国古代称直角三角形中较短的直角边为勾，较长的直角边为股，斜边为弦。因而得名。亦称商高定理。国外通常称“毕达哥拉斯(Pythagoras，前580—前500) 定理”。法国、意大利等国称“驴桥定理”。《周髀算经》开篇就给出勾股定理的一个特例：“故折矩，以为句广三，股修四，径隅五。”这是约公元前11世纪周公与商高的对话。接着在陈子测日法中给出其一般形式：“以日下为勾，日高为股，勾、股各自乘，并而开方除之，得邪至日(观测者到太阳的距离)。”可见中国古代先民对勾股定理的认识十分久远。三国时赵爽在《勾股圆方图注》中、刘徽在《九章算术注》中都给出了证明。勾股定理在中国古代传统数学中占有十分重要的地位。许多问题的研究和理论的形成都是围绕勾股定理而展开、发展的。数千年来已逐渐形成了以勾股定理及其应用为核心的中国式几何学。

勾股定理gougu dingli

直角三角形两直角边的平方和等于斜边的平方.如图1，在△ABC中，

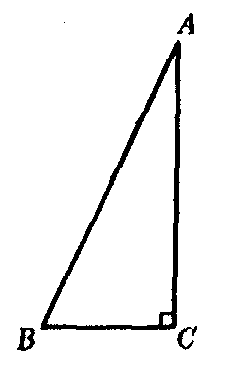
图1

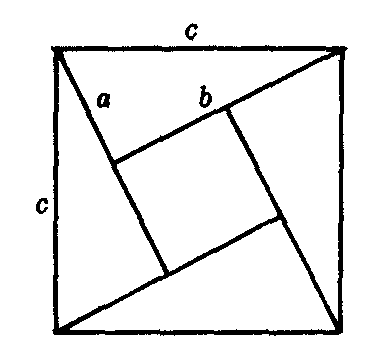
图2

∠C=90°，则AC²+BC²＝AB².
我国古代把直角三角形的较短的直角边称为勾，较长的直角边称为股，斜边称为弦.

勾方+股方=弦方.

这个定理称为勾股定理，勾股定理的证明，最早见于《周髀算经》赵君卿注里.据记载，周朝商高就谈到“勾玄三，股修四，径隅五.”就是“勾三、股四、弦五”之说，所以勾股定理也称商高定理.
这个定理也称为毕达哥拉斯定理.
勾股定理证明方法很多，如赵君卿注里记载的证法如图2.2ab+(b-a)²＝c²，化简为a²+b²＝c².
类似以上拼图或分割的方法还有很多.如图3,(a+b)²-2ab=c²，化简为a²+b²＝c².

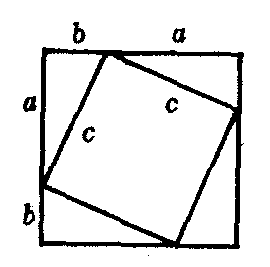
图3

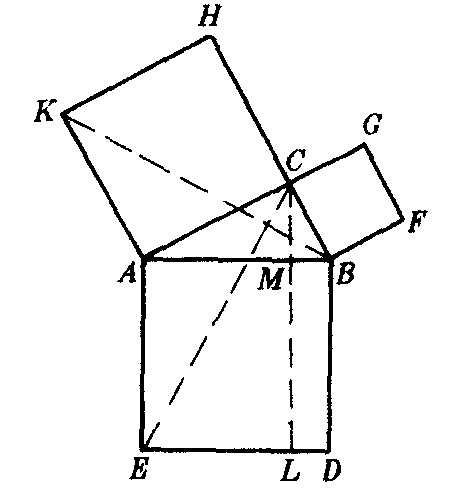
图4

欧几里得《原本》中是用全等三角形和面积证明的.如图4，在△ABC中，∠ACB=90°，分别以AB,BC,CA为边向三角形外作正方形ABDE,BFGC,CHKA.作CL⊥DE于L，交AB于M.可证△AEC≌△ABK，矩形AELM=2△AEC，正方形CHKA=2△ABK，因此，矩形AELM=正方形CHKA.同理矩形BMLD=正方形BFGC.正方形CHKA+正方形BFGC=正方形ABDE，即AC²+BC²＝AB².

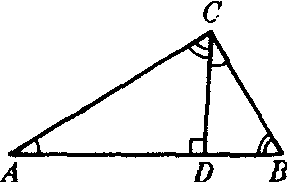
勾股定理还可以用相似三角形等方法证明.如图5，在△ABC中，∠ACB=90°，作CD⊥AB于D，可证△ADC∽△ACB.AC:AB=AD:AC,AC²
＝AB·AD，同理可证BC²＝AB·BD，所以AC²+BC²＝AB (AD+BD)，即AC²+BC²＝AB².

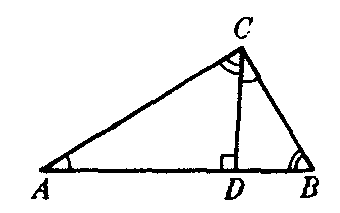
图5

勾股定理

又称“毕达哥拉斯定理”。直角三角形斜边的平方等于两条直角边的平方和。最早出现于《周髀算经》中。

勾股定理

Pythagorean(/Pythagoras')theorem