关于直线的对称变换
关于直线的对称变换guanyu zhixian de duicheng bian-huan
亦称关于直线的反射变换.几何变换的一种.从一点P向直线l引垂线,垂足为O,延长PO到P′,使|OP′|=|OP|,则称点P′为点P关于直线l对称的像点,也称对称点,称直线l为对称轴.这种把平面上每一点都变到它关于某直线的对称像点的平面到自身的变换,叫做关于直线的对称变换.在平面直角坐标系中,关于X轴的对称变换可以用公式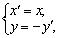
| 来表示. |
若一个图形M上的每一点关于直线l的像点组成图形M′,则称图形M经过关于直线l的对称变换得到图形M′.若一个图形经过关于某一条直线的对称变换变为它自身,则称这个图形是关于这条直线的对称图形.例如,等腰三角形是关于它的底边上的高(或中线,或顶角平分线)所在直线的对称图形.圆是关于它的任意一条直径所在直线的对称图形.
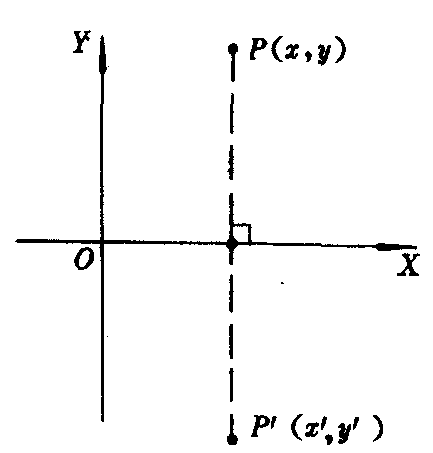
注意:平面上的对称变换,不能通过图形在平面上的移动来实现,它可以经过翻折后在平面上移动来实现,这是空间的移动.
☚ 恒等变换 关于直线的对称变换的性质 ☛
- 江加良是什么意思
- 江加走是什么意思
- 江动月移石 溪虚云傍花是什么意思
- 江势是什么意思
- 江势猛是什么意思
- 江勇为是什么意思
- 江勺子是什么意思
- 江化南是什么意思
- 江北是什么意思
- 江北不如南地暖,江南好断北人肠。是什么意思
- 江北人是什么意思
- 江北佬是什么意思
- 江北化工城是什么意思
- 江北区旅游局是什么意思
- 江北区(寸滩街道)是什么意思
- 江北厅志是什么意思
- 江北县国术馆是什么意思
- 江北大营是什么意思
- 江北戏是什么意思
- 江北按察使是什么意思
- 江北捍海堰是什么意思
- 江北提督是什么意思
- 江北教案是什么意思
- 江北文脉是什么意思
- 江北棚棚是什么意思
- 江北淮东道肃政廉访司是什么意思
- 江北烟光里,淮南胜事多。是什么意思
- 江北煤港是什么意思
- 江北熊鸭子是什么意思
- 江北秋阴一半开,晚云含雨却低徊。青山缭绕疑无路,忽见千帆隐映来。是什么意思
- 江北窦子是什么意思
- 江北老是什么意思
- 江北运程是什么意思
- 江午坡集是什么意思
- 江华是什么意思
- 江华何氏建筑群是什么意思
- 江华凌云塔是什么意思
- 江华县是什么意思
- 江华县学是什么意思
- 江华县志是什么意思
- 江华县旅游局是什么意思
- 江华县统计局关于2002年国民经济和社会发展统计公报是什么意思
- 江华岛是什么意思
- 江华廷是什么意思
- 江华故城是什么意思
- 江华文庙是什么意思
- 江华本是什么意思
- 江华条约是什么意思
- 江华林业采育场是什么意思
- 江华毛尖是什么意思
- 江华瑶家“八宝被”是什么意思
- 江华瑶族自治县是什么意思
- 江华瑶族自治县电影第一队是什么意思
- 江华瑶族自治县自治条例是什么意思
- 江华瑶族自治县(沱江镇)是什么意思
- 江华瑶民起义是什么意思
- 江华瞄准两广市场开发农业是什么意思
- 江华米粉肉是什么意思
- 江华苦茶是什么意思
- 江华西佛桥是什么意思