兔子问题Tuzi wenti

在意大利数学家斐波那契(Fibonacci, L.，参见该条)的《算书》(1202)中，有许多有趣的题目。最著名也最重要的，是下面的“兔子问题”：
有人想知道在一年中一对兔子可以繁殖成多少对，就筑了墙把一对兔子放在里面。如果每对大兔每月生一对小兔，而每对小兔生长一个月就成为大兔，并且所有的兔子全部存活， 那么一年后围墙中有多少对兔子？
我们用△表示一对初生的小兔， 用口表示一对一月龄的大兔， 用○表示一对二月龄以上、正在繁殖的兔子，假定1月1日把一对小兔放进围墙， 那么兔子生长、繁殖的规律可以用下图表示：
可以看出，从第三个月起，每月兔子的对数都等于前两个月的和。这个规律可以任意递推下去。如果记第n个月兔子的对数为U_n, 那么：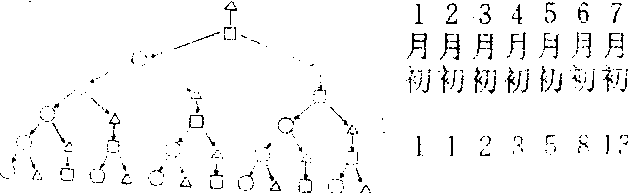
u1=u₂＝1
un₊₂₌un+₁+u_n (n=1, 2, 3, ……)
把这些数的前13个写出来就是
1, 1,2,3,5, 8,13,21,34,55,89,144,233，也就是说，到下一年的1月初，围墙里就有了233对兔子， 这就是问题的答案。
这个数列显然可以任意多项地写下去， 现在人们称之为“斐波那契数列”，其中的数就称为“斐波那契数”。它的通项公式为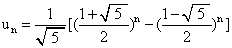
一个各项均为整数的数列，其通项却要用无理数的幂来表示。这实在是很令人惊讶了，进一步的计算可以得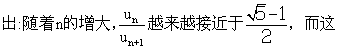
个数恰好就是众所周知的 “黄金分割数”。
斐波那契数列有许多奇妙的性质， 例如：(1)斐波那契数列中任意相邻的两项互素；(2)u₁+u₂+……+u_n＝u_n+₂-1
(n=1, 2, 3, ……)
(3)un+₁un-₁-u2n=(-1)ⁿ (n≥2)
(4)u_2n+_1=u2n+1+u2n (n=1, 2, 3, ……)
(5)u₂n=un (un+₁+un-₁) (n≥2)
(6)um+n=un+1um+unum+1 (m、n是自然数)
斐波那契数列在数学的各个领域里有许多意想不到的应用。例如， 关于辗转相除法， 法国数学家拉梅(Lame, G.,1795-1870)曾证明：为了求出两个正整数的最大公因数，所需进行的除法的次数决不大于较小整数的位数的5倍，例如对于2位数，所需进行的除法不会超过10次。这个巧妙的定理的证明首先要用到斐波那契数列的某些性质。对于本世纪提出的一个有趣的数学难题： 利用边长为连续自然数 (1, 2, 3，……)而无一重复的正方形可否盖住整个平面，根据斐波那契数列的性质已经证明： 它们至少可以盖住平面的3/4。此外， 由于斐波那契数与黄金分割数之间的密切关系， 它在优选法中的应用早已是众所周知的了。
斐波那契数列还令人难以置信地广泛出现在自然界中，例如，我们考虑向日葵的花盘。从盘中心向外辐射出来的螺线弧把花盘分割为含有花籽的菱形小块。如果数一下顺时针方向伸展的螺线， 再数逆时针方向伸展的螺线，会发现两个数目是斐波那契数列的两个邻项。事实上，任何菊科植物的花盘都有这一特性。我们再来考虑从 一些植物的主茎（例如树木的主干） 的侧面生长出来的叶子(或芽体、枝叉)，如果在主茎底部附近选定一片叶子，然后沿主茎向上计数叶子，一直数到恰好在选定叶子正上方的 一片为止， 这个数通常是斐波那契数列中的一项， 在沿主茎向上计数叶片的同时，如果还计数绕主茎施转的圈数，也刚好数到刚才那片叶子为止， 所得到的通常是斐波那契数列中刚才那项的前一项。在给多种类的植物中都可以看出类似的排列形式，例如莴苣头上的叶子，洋葱的层次和松果的圆锥螺线等。
斐波那契数列到处可见，应用层出不穷，有关的新发现以快得惊人的速度增加。于是，1963年在美国成立了斐波那契协会， 并开始出版主要研究斐波那契数列和其他有关数列的杂志《斐波那契季刊》。在创刊的头三年中，它发表了近1 000页有关的研究成果。1968年，为了解决大量稿件的积压问题，出版了三期增刊。这一盛况一直持续不衰。
与斐波那契的兔子问题类似，14世纪印度一位数学家纳拉亚那 (Narayana) 提出了 “母牛问题”：
有一头母牛，它每年年初生一头小母牛，每头小母牛从第4年起， 每年年初也生 一头小母牛， 有学识的人， 请告诉我， 在第20年里， 牛的头数共有多少？
由题目所给的条件， 我们知道在第一年年初已经有了一头大母牛和一头刚生的小母牛， 请读者写出这一数列的前20项和牛数增加的规律。