Pareto有效点的存在性

---

设X，Y是二个线性空间，A，B分别为X，Y的非空子集，C是Y中的非空凸锥，f：A→Y。

对y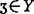，定义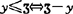∈c。B的Pareto有效点、次有效点集分别为E(B，C)=｛y∈B｜不存在z∈B，z≠y使z≤y｝，N(B，C)=｛y∈B｜不存在z∈B使y≤z，z≤y｝，对向量最优化问题(Vp)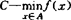：，其有效解、次有效解集分别为E(f，c)=｛x∈A｜f(x)∈E(f(A)，C)｝，N(f，c)=｛x∈A｜f(x)∈N(f(A)，C)｝，考虑(Vp)的有效解、次有效解的存在性，通常是先考虑B，C满足什么条件时，E(B，C)，N(B，C)非空，再考虑f，A满足什么条件，f(A)具有前面对B的要求。

1974年游(P．L．Yu)说明若Y=R^m，C是锐的，B紧，则E(B，C)≠Φ。随后许多学者围绕这基本定理进行研究。

这些研究主要是从以下几个方面展开的：(1)讨论其它非控点的存在性。(2)向无限维空间拓广。(3)减弱关于C的尖性假设。(4)减弱B的紧性假设。

(5)建立函数的锥连续性概念，配以A的某种紧性，以期实现f(A)具有所希望的紧性。从证明方法看，主要是借用纯量化方法或借用Zorn引理，仅有个别结论是借助不动点定理来证明的。代表性的工作主要有：

1978年哈特利(R．Hartley)对y∈Y，记截割By=(y－c)∩B，称B是C－截割紧的，如对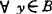，By紧，说明若Y=R^m，B是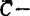截割紧的，则N(B，C)≠Φ，围绕它，在有限维空间，比曾(G．R．Bitran，1979)等、汉尼格(M．I．Henig，1982)、沙哇拉吉(Y．Sawaragi，1985)等借用退化锥反映B的锥有界性，再辅以B的某种锥闭性去代替前面B的锥紧性导出了几个存在性定理。后又被梅家骝(1987)改进为若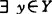使(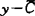)∩B非空紧，则N(B，C)∩(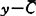)≠Φ，波温(J．M．Borwein，1983)对Y为可分拓扑线性空间时，说明若C是闭凸锥且B是C－截割紧的，则N(B，C)≠Φ，这结论又被斯特拉－卡瓦(A．SternaKarwat，1986，1987)拓广为若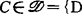为Y中的凸锥｜对Y的每个闭子空间L，如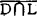是子空间，则D∩L也是子空间｝，B是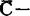截割紧，则N(B，C)≠Φ。

1978年西塞利(L．Cesari)等设Y为Banach空间，称C满足π－性质，如｛a∈Y^*＼｛0｝｜对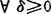，｛y∈C｜a(y)≥－δ｝弱紧｝≠Φ。称B下有界，如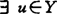使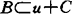证明了如闭凸锥C满足π－性质，B下有界，则弱C－有效点w－inf(B，C)=｛x∈w－c1B｜(x－C＼｛0｝)∩B=Φ｝≠Φ，如B还是弱闭的，则E(B，C)≠Φ。龚循华(1988)将其改进为若Y是自反Banach空间，C是锐闭凸锥，C又是正规的(即Y中任意序区间都范数有界)，B有下界，则w－inf(B，C)≠Φ。

他1990年又引进了一种拟π－性质概念，用以说明有效点的存在性，斯台(T．Staib，1988)设C为闭凸锥，说明了如Y=R^m，B有界，则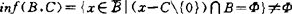，如Y是自反Banach空间，B凸且有界，则inf(B，C)≠Φ，如Y是可分拓扑线性空间，C点式，B是C截割弱紧的，则_inf(B，C)≠Φ。

1980年柯里(H．W．Corley)设Y是Banach空间，称B是C－半紧的，如B的任意形如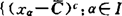，x_α∈B｝的复盖均有有限子覆盖，称f：A→Y是C－下半连续的，如对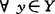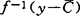，是闭的。设C为尖闭凸锥，说明了如B是C－半紧的，则E(B，C)≠Φ，如A紧，f是C－下半连续的，则E(f，C)≠Φ。

塞柯尼(J．P．Cecconi，1986)说明其中关于C闭的假设可去掉。汉尼格(1982，1986)、本森(H．P．Benson，1983)、沙哇拉吉(1985)等说明若Y=R^m，C为点式闭凸锥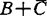，闭，B+C凸，则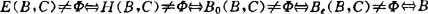满足控制性质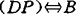是C－半紧的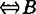是C－截割紧的，其中H(B，C)，B₀(B，C)，Be(B，C)分别是B的汉尼格、波温、本森真有效点集。

龚循华(1990)设Y是Banach空间，C为点式闭凸锥，说明如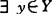使By是C－半紧的，则E(B，C)≠Φ。

1983年波温设Y为可分拓扑线性空间，称C具有Daniell性质，如Y中每个有下界的减网收敛于它的下确界，说明了如C是闭凸锥且具有Daniell性质，B又有一个有下界的闭截割，则N(B，C)≠Φ。

1984年赵(K．L．Chew)设Y是Banach空间，称B是C－归纳的，如B关于C的非空截割全序链的交非空。说明了若C是点式凸锥，B是C－归纳的，则E(B，C)≠Φ。

如C是凸锥，C∩(－C)闭，B是C－归纳的，则N(B，C)≠Φ。1986年杨(J．Jahn)设Y是自反Banach空间，C是点式凸锥，范数‖·‖_y在C上强单调递增(即u，v∈C，u≠V，u≤v隐涵‖u‖＜‖v‖)，说明若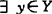使By弱闭且有下界，则E(B，C)≠Φ，若intC≠Φ，B弱闭且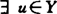使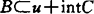，则Be(B，C)≠Φ。另外，杨还讨论了弱有效点的存在性。

1989年鲁克(D．T．Luc)进一步拓广了波温和杨所得的结果。

他设Y是一个实拓扑线性空间，C是凸锥，称Y中一个网｛x_α：α∈I｝是减网，如对α，β∈I，β＞α有x_α＞x_β(指x_α≥x_β但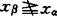）。称B是C－完备的，如不存在形如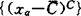的对B的覆盖，其中｛x_α｝是B中的一个减网。

称C是校正的，如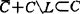，L=C∩－C。说明了如C是校正凸锥，那么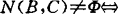B有一个非空C－完备截割。

如B是C－完备的，C是校正凸锥，那么B满足控制性质。

设Y=R^m，E(B，C)≠Φ，B的有效极点集E_B=E(B，C)∩extB，其中extB为B的极点集，游(1975)说明若C为凸锥，B是紧多面凸集，则E_B≠Φ。波温(1983)说明若C为闭凸锥，B为紧凸集，则E_B≠Φ。梅家骝(1991)说明若0∈C，C在0点凸(C不一定凸也不一定是锥)。

B是不含直线的闭凸集(或B是紧集，｛a｜＜a，x＞＜0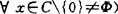，，则E_B≠Φ。

对e∈C＼｛0｝，定义B的e－有效点集e－E(B，C)=｛x∈B｜(x－e－c＼｛0｝)∩B=Φ｝。斯台(1988)说明若Y是可分拓扑线性空间，C是点式闭凸锥，B有界(或有下界，或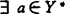使a(y)≥0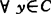，，a(e)＞0且infa(B)＞－∞｝，则e－E(B，C)≠Φ。

对集值映射F：A→2^Y，柯里(1987)定义N(F，C)=｛x∈A｜F(x)∩N(F(A)，C)≠Φ｝，讨论了这种次有效解的存在性，鲁克(1989)设Y是可分拓扑线性空间，称F在A上C－上连续，如对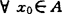，F(x₀)的任意邻域V，存在x₀的邻域∪使，。

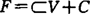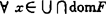他设F在A上C－上连续，A紧，C为凸锥，说明若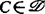，F是紧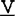值的，则N(F，C)≠Φ。若C是校正的，F是C－半紧－值的(或对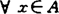，F(x)+C是闭的，C－完备的)则N(F，C)≠Φ。

目前在减弱C的凸性假设方面的工作尚不多见。这可能是由于C不凸就意味著序关系缺少传递性，因而证明存在性定理时最有力的工具Zorn引理不能使用，从而给问题讨论带来困难，但这必竟是一个值得研究的问题。

。【参考文献】：

1 Yu P L. J Optim Theory Appl, 1974,14,319～377

2 HartleyR. SIAM J Appl Math,1978,34:211～222

3 Cesari L, et al. Trans Amer Math Soc, 1978,244:37～65

4 Corley H W. J Optim Theory Appl, 1980,31:277～281

5 Borwein J M. Math Oper Res,1983,3:64～73

6 Chew K L. J Optim Theory Appl, 1984,44:1～ 53

7 Jahn J. Mathematical vector optimization in partially ordered linear spaces. Verlag Peter Lang Gmbh Frankfurt and Main, 1986

8 StaibT. JOptimTheoryAppl,1988,59:289～306

9 Luc D T. Lecture notes in economics and mathematical systems 319. Springer-verlag,1989

10 梅家骝．系统科学与数学，1991，11∶313～319

(南昌大学梅家骝教授撰；李宗元审)

上一篇：Klein群的有限性定理
下一篇：现代科技综述大辞典上目录

"ParisParis

---

[′pr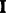s]〈名词〉巴黎

Paris is a beautiful city．巴黎是一座美丽的城市。