两直线相关系数的比较与合并

样本直线相关系数r与总体相关系数ρ=0比较，经假设检验，认为有相关，才能和其他相关系数比较。比较可分两种情况： 一是样本相关系数与总体相关系数 ρ=C (C为一已知不为零且其绝对值小于1的常数) 的比较，目的在于推断r是否来自ρ=C的总体；二是两样本相关系数r1与r2的比较，目的是推断两总体相关系数有无差别。无论是哪一种，都要先将r作反双曲正切tanh-1变换，得到z值，然后用z作u检验。检验结果若接受ρ=C的假设，认为ρ与C没有差别，r来自ρ=C的总体；若接受ρ₁＝ρ2的假设，认为ρ₁ 、ρ2间没有差别，则需要时可合并为一个相关系数；若拒绝ρ1=ρ2，则认为ρ₁≠ρ2,ρ₁、ρ2间有差别，则不能合并。
反双曲正切变换 又称z变换。r值的抽样分布与样本含量n及ρ的大小有关。由图1可见： 当ρ=0时，r值是一个对称于r=0的分布，当 ρ≠0且n不太大时，r值呈偏态分布。ρ愈接近1(或-1)，偏度愈大。由图1可见：ρ=0.8,n=8时，r的分布是一很偏的曲线，随着n的增大，这种不对称程度将逐步减少。对于ρ≠0,R. A. Fisher提出用式(1)进行变换，

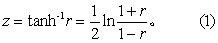
当n较大，比如n≥20时，变换后的z值近似地服从以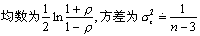的正态分布，见图2。由于σz₂仅与样本含量有关，故z值的分布曲线的形态与ρ的大小无关。统计书中有r与z的对照表可查，亦可用有双曲函数的电子计算器算得。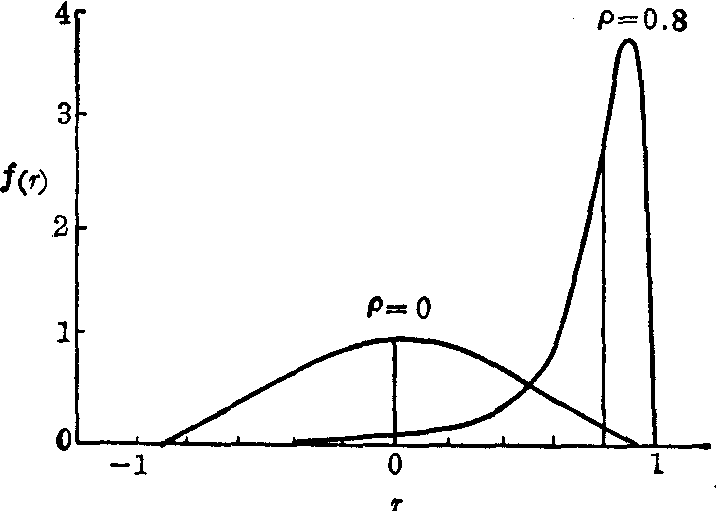

图1 相关系数r值的分布

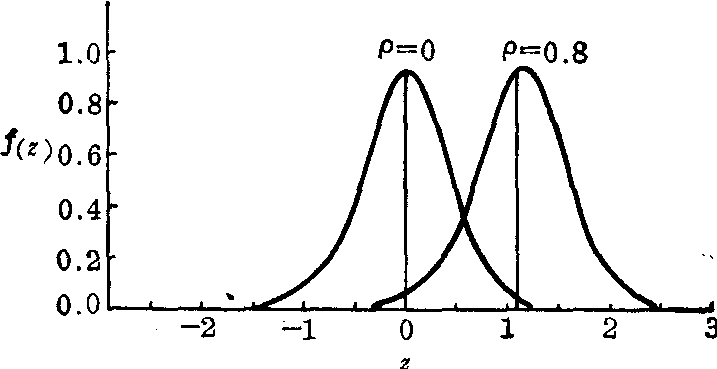
图2 z值的分布

样本相关系数与总体相关系数(ρ=C)的比较 用u检验。检验假设H0为ρ=C。将r及C按式(1)作z变换，然后代入式(2)计算u值。查u界值表得P值作出推断结论。若接受ρ=C，则认为该样本来自ρ=C 的总体，否则不是。

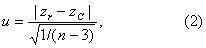
式中z_r、z_C分别为r、C的z变换值，n为样本含量。两直线相关系数的比较 用u检验。检验假设H₀为两总体相关系数相等，即ρ₁ =ρ₂，先将r₁、r₂作z变换，代入式(3)求u。

式中分母为两z值差的标准误。查u界值表得P值，按所取检验水准作出推断结论。若不拒绝H₀，则认为ρ₁与ρ₂间无差别，可将两样本资料合并；若拒绝H0则认为两相关系数间有差别，不能合并。
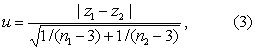
两直线相关系数的合并 即求两相关系数的加权均数rw。先将两相关系数进行z变换；再代入式(4)求z的加权均数z_w

然后查r与z的对照表，或用有双曲函数的电子计算器，求对应于z_w的双曲正切函数值rw。
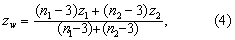
例1 某地测量18～25岁女青年50人的体重与体表面积，得相关系数为0.9174，问该样本相关系数是否来自ρ=0.8的总体？
H₀: ρ=0.8,
H₁: ρ>0.8。
单侧a=0.05。
今r=0. 9174,C=0.8。

查u界值表得P<0.005，按a=0.05水准拒绝H₀，接受H_1,可认为ρ>0.8，即该样本不是来自ρ=0.8的总体。
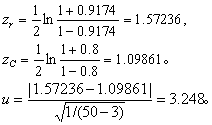
例2 某地测定了部分健康成人皮肤氧分压与动脉氧分压，并求得相关系数为：男23人，r = 0.776；女14人，r= 0.766。试比较男、女两相关系数有无差别？ 若无差别则合并之。
H₀: ρ₁ =ρ₂
H₁: ρ1≠ρ_2。
a =0.05。

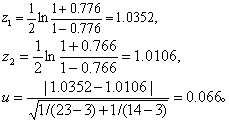
查u界值表得P>0.50，按a=0.05水准不拒绝H₀，可认为两相关系数无差别。可合并按式(4)，得

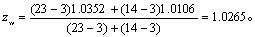
求此值的双曲正切函数值得r=0.7725，即合并的加权相关系数。