不定积分的第一换元积分法buding jifen de diyi huanyuan jifenfa

设(x)是可导函数，则根据换元公式

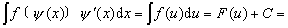
F[(x)]+C

求不定积分的过程叫做第一换元积分法.
第一换元积分法的基本思路如下. 若所求的不定积分∫g(x) dx不易计算，而g(x)含有因子ψ′ (x)，使g (x)可以表示成ψ′ (x)与ψ (x) 的某个函数f(ψ (x)]的乘积，或g (x) dx=f [ψ (x)]ψ′ (x) d x=f [ψ (x)] dψ (x)，则可作变换u=ψ (x)，得

而

⨜f(u)du

容易求，且等于F (u) +C，则根据上述法则，得

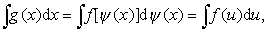
⨜f(u)du=F(u)+C=F[⨜(x)]+C.

这就是所求的

⨜g(x)dx.

简言之，第一换元积分法是指，
通过适当的变量代换，即选取原被积函数的某个中间变量为新的积分变量，将所求的不定积分化为易求的基本形式，而后再求出积分结果.
第一换元积分法又称“凑微分法”，方法的关键在于找到符合要求的ψ(x):不仅能将原被积表达式凑成f (ψ(x)]dψ(x)的形式，更重要的是使得到的 ∫f (u)du易于求出.
例1 求
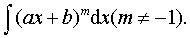
解 可设u=ax+b，则du=adx,dx=1/adu.

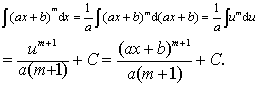
例2 求
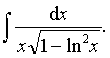
解 可将1nx作为中间变量，于是d1nx=dx/x.