空间中是否存在电场及电场各处的情况原则上可用检验点电荷q0来检测。
描述电场的基本物理量之一是电场强度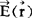 ,其物理意义是:当q0置于
,其物理意义是:当q0置于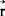 处时其所受电场的力为
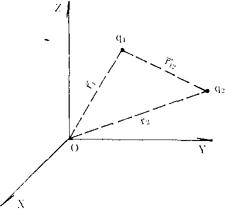
处时其所受电场的力为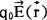 。库仑定律是电学中最基本的定律之一,即实验上发现,两个点电荷q1及q2的相互作用力显示为同性相斥异性相吸(力的方向在q1与q2的连线方向),力的数值与距离平方成反比,例如q2所受力写成
。库仑定律是电学中最基本的定律之一,即实验上发现,两个点电荷q1及q2的相互作用力显示为同性相斥异性相吸(力的方向在q1与q2的连线方向),力的数值与距离平方成反比,例如q2所受力写成
或写成
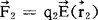 (2)
(2)
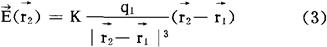
(3)式即表示点电荷q1在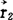 处产生的电场强度,其中k是取决于单位制的普适常数。
处产生的电场强度,其中k是取决于单位制的普适常数。
在(3)式的基础上,不难推知非单个点电荷的带电体系所产生的电场强度为

因为可以证明,电场力是有势的,所以也常用物理量电位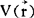 来描述电场。
来描述电场。
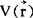 的物理意义是:置于
的物理意义是:置于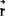 的检验电荷q0的电位能为
的检验电荷q0的电位能为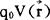 。
。
若把无限远处定为零电位点,则可得

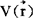 与
与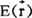 的关系为
的关系为
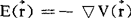 (6)
(6)
如(4)及(5)式所示,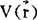 的计算常比
的计算常比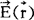 的计算简单一些,故有时常先计算
的计算简单一些,故有时常先计算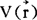 ,尔后利用(6)式算
,尔后利用(6)式算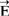
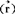 。
。
可以证明,真空中的静电场中各点的电位满足泊松方程

式中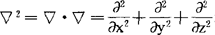 称为拉普拉斯算符,ε0为真空介电常数(又称真空电容率),
称为拉普拉斯算符,ε0为真空介电常数(又称真空电容率),
ε0=8.85419×10-12库仑2/牛顿·米2 (7)
对于体电荷密度ρ=0的地方,(7)式变为拉普拉斯方程
▽2V=0 (8)
分析介质中的静电场,因计入介质受电场作用后会发生极化而诱生的极化电荷,可推知各向同性的均匀介质中的泊松方程为

式中εr为介质的相对介电常数(简称介电常数)。
因此,静电学的基本任务之一——计算V及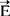 ,也可归结为结合边界条件解方程(7)、(8)或(9)。
,也可归结为结合边界条件解方程(7)、(8)或(9)。
对于某一具体问题,无论是从(5)式计算,还是由结合边界条件解方程计算,原则上应得到相同的结果,但计算易难可大不一样,为此,应在计算前慎加选择。
- rajmahal是什么意思
- rajnarain是什么意思
- rajneesh,bhagava shree是什么意思
- rajni是什么意思
- rajnikanth bordoloi是什么意思
- rajpurohit是什么意思
- rajput是什么意思
- rajputana是什么意思
- rajput girodar是什么意思
- rajput miniatures是什么意思
- rajputs是什么意思
- rajput song of war是什么意思
- rajputs 拉杰普特人是什么意思
- rajshahi是什么意思
- rajshahi association是什么意思
- rajshekar是什么意思
- rajsooya yajna是什么意思
- rajuka是什么意思
- raju pulla thirupati是什么意思
- rajya是什么意思
- rajyapala pratihara是什么意思
- rajya sabha是什么意思
- rajyavarddhana是什么意思
- rajyavardhana是什么意思
- rajyonarayan basu是什么意思
- rak是什么意思
- raka ⅰ是什么意思
- raka ⅱ是什么意思
- rake是什么意思
- rakhakaras是什么意思
- rakhi是什么意思
- rakhi bandha是什么意思
- rakkushi是什么意思
- rakoczy ⅱ ,ferenc是什么意思
- rakrak是什么意思
- raksa是什么意思
- raksas是什么意思
- raksasa是什么意思
- raksasagraha是什么意思
- raksasas是什么意思
- raksasayajna (raksasasatra)是什么意思
- raksasa ⅰ是什么意思
- raksasa ⅱ是什么意思
- rakshabandhan是什么意思
- rakshan-bandhan是什么意思
- rakshasa charvaka是什么意思
- rakshasi是什么意思
- raksita是什么意思
- raksobhaksa是什么意思
- raksobhaksam是什么意思
- raksovaha是什么意思
- rakta是什么意思
- raktabija是什么意思
- raktaja是什么意思
- raktakarabee(raktakaravi)是什么意思
- raktanga是什么意思
- raktesvari是什么意思
- ra lata是什么意思
- raleigh是什么意思
- raleigh,sir walter是什么意思