随机过程

---

设给定概率空间(Ω，F，P)及指标集T，对每一tεT，有定义在(Ω，F，P)上的随机变量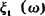，ωεΩ，与之对应，则称依赖于t的一族随机变量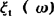为随机过程。

可用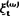｛，tεT｝表示。其中t称为参数或时间，T称为参数集，是一个无穷的集合。最常见的有：(1)T₁=｛0，1，2，…｝；(2)T₂=｛…，－3，－2，－1，0，1，2，3……｝；(3)T₃=［a，b］其中a、b可以是±∞。当T为前两种情形时，也称为随机序列，属于离散型；后者属于连续型。随机过程的理论产生于本世纪初期，是由于物理学、生物学、通讯与控制，以及管理科学等方面的需要而逐步发展起来的。