8.4.1 二重积分
二重积分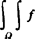 (x,y)dxdy的计算公式(积分限应从小到大):
(x,y)dxdy的计算公式(积分限应从小到大):
直角坐标系下
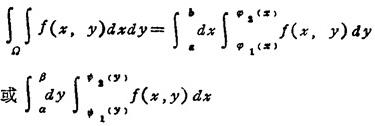
极坐标系下,设x=ρcosφ,y=Psinφ,则
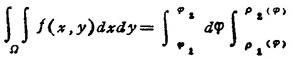
f(ρcos中,ρsinφ)PdP
二重积分的变量替换(雅可比式):{x=x(“,v)
设连续可微函数,把平面Oxy上y=y(u,v)的有界闭区域Ω单值映射到平面O′uv的闭区域Ω′,其雅可比式为
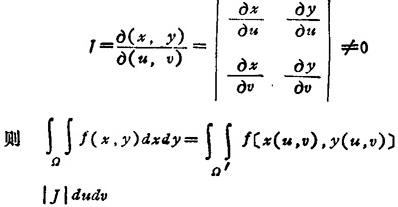
8.4.2 三重积分
三重积分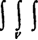 f(x,y,z)dxdydz的计算式:
f(x,y,z)dxdydz的计算式:
设有界闭区域V由下列不等式确定:
α≤x≤b,y1(x)≤y≤y2(x),z1(x,y)≤z≤z2(x,y)
❶ 直角坐标系
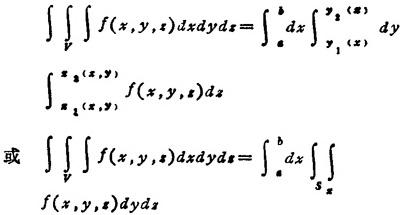
式中 Sx是用平行于Oyz的平面截V所得截面。
❷ 圆柱坐标系
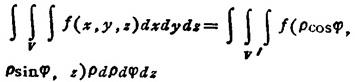
式中 V′是区域V在圆柱坐标系中的表达式。一般地,0≤φ≤2π。
❸ 球面坐标系
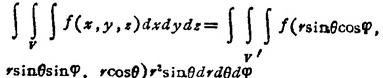
式中 V′是区域V在球面坐标系中的表达式;θ为r与z轴的夹角。一般地,0≤φ≤2π,0≤θ≤π。
三重积分的变量替换(雅可比式):

把Oxyz空间的有界闭域V双方单值映射到O′uvω空间的闭域V′,且当(u,v,ω)∈V′时,其雅可比式
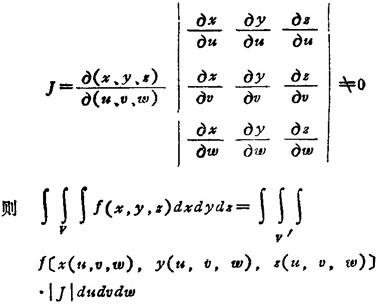
- 附:点穴疗法是什么意思
- 附:癫痫持续状态是什么意思
- 附:第一国际临时委员会是什么意思
- 附:第一国际解散宣言是什么意思
- 附:美国垄断财团表是什么意思
- 附:脑梗死诊断标准是什么意思
- 附:蔬菜上几种潜叶蝇的识别是什么意思
- 附:近代时期部分殖民战争表是什么意思
- 附:部分国家的国内战争表是什么意思
- 附:部分国家的民族解放战争表是什么意思
- 附:酸性红87铝色淀是什么意思
- 附:重症肌无力危象发作是什么意思
- 附:*食品红14铝色淀是什么意思
- 附:食品香精是什么意思
- 附:马立克氏病细胞结合性疫苗的正确管理与使用是什么意思
- 陆丰市是什么意思
- 陆奥宗光是什么意思
- 陆学士杂着是什么意思
- 陆定一是什么意思
- 陆川县是什么意思
- 陆树声《茶寮记》有什么内容是什么意思
- 陆河县是什么意思
- 陆游是什么意思
- 陆生动物是什么意思
- 陆生植物饵料的营养成分是什么意思
- 陆瘦燕针灸论着医案选是什么意思
- 陆羽《茶经》的内容是什么是什么意思
- 陆羽如何品评天下水是什么意思
- 陆良县是什么意思
- 陆诒是什么意思
- 陆贾着书是什么意思
- 陆辑崇奢论是什么意思
- 陆辑崇奢论是什么意思
- 陇中人如何喝罐罐茶是什么意思
- 陇川县是什么意思
- 陇西县是什么意思
- 陇首(1)是什么意思
- 陈与义是什么意思
- 陈启着是什么意思
- 陈寿着书处是什么意思
- 陈巴尔虎旗是什么意思
- 陈师道是什么意思
- 陈廷骅是什么意思
- 陈旧性外阴Ⅲ度裂伤是什么意思
- 陈旧性胸腰椎损伤合并脊髓损伤的治疗是什么意思
- 陈旧性脊髓损伤的处理是什么意思
- 陈旧性脊髓损伤的移植治疗是什么意思
- 陈旧性脊髓损伤的诊断是什么意思
- 陈旧性颈椎损伤合并颈髓损伤的治疗是什么意思
- 陈泽富是什么意思
- 陈煚是什么意思
- 陈玉书是什么意思
- 陈留市隐(1)(并序)是什么意思
- 陈皮是什么意思
- 陈皮是什么意思
- 陈着是什么意思
- 陈锡桥是什么意思
- 陌上桑是什么意思
- 降低不良品损失工作法是什么意思
- 降低卷烟焦油量的方法是什么意思