亦称“分派问题”。
应用于合理分配资源或制订合理的工作分派方案,使所得最大或所费最少。它是又一类重要的线性规划专门问题。
设有m种资源A1,A2,…,Am,另有n项“活动”(任务)B1,B2,…,Bn。
由于“活动”的性质各异,每种资源完成某项“活动”所产生的效能或效益亦不尽相同。
若已知资源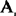 完成“活动”Bj产生的效益为Cij,在完全分配的情况下(即m=n),即每一种资源能够而且只能够分配担当一项“活动”时,应如何分配资源才能使之产生的总效益为最佳。如果这种效益是指完成任务所需工时或费用而言,就是最小分配问题,若是指完成任务的价值来说,就是最大分配问题。
完成“活动”Bj产生的效益为Cij,在完全分配的情况下(即m=n),即每一种资源能够而且只能够分配担当一项“活动”时,应如何分配资源才能使之产生的总效益为最佳。如果这种效益是指完成任务所需工时或费用而言,就是最小分配问题,若是指完成任务的价值来说,就是最大分配问题。
它们的数学模型是:
给定一个效益矩阵:
C=(Cij)m×n,
求一个分派矩阵:
X=(Xij)m×n,
满足约束条件:
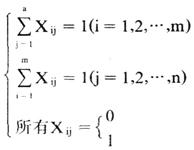
使得目标函数达到:
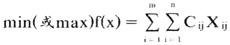
- 茶里放盐是什么意思
- 茶鈐是什么意思
- 茶銀是什么意思
- 茶钟是什么意思
- 茶钤是什么意思
- 茶钱是什么意思
- 茶钴是什么意思
- 茶钵是什么意思
- 茶铛是什么意思
- 茶铫是什么意思
- 茶铫子是什么意思
- 茶银是什么意思
- 茶银尺蠖是什么意思
- 茶铺是什么意思
- 茶铺头的龙门阵——想到哪儿说到哪儿是什么意思
- 茶铺子里的水是什么意思
- 茶铺子里的水——滚开是什么意思
- 茶铺搬家——另起炉灶是什么意思
- 茶铺里招手——胡(壶)来是什么意思
- 茶锅头是什么意思
- 茶锈是什么意思
- 茶镣是什么意思
- 茶长绵蚧是什么意思
- 茶阑酒尾是什么意思
- 茶阵是什么意思
- 茶陵军是什么意思
- 茶陵县是什么意思
- 茶陵县列宁高级中学是什么意思
- 茶陵县城关镇是什么意思
- 茶陵县工农兵政府是什么意思
- 茶陵县工农兵政府旧址是什么意思
- 茶陵县广播电台是什么意思
- 茶陵县志是什么意思
- 茶陵县第一中学是什么意思
- 茶陵县(城关镇)是什么意思
- 茶陵县(州)署衙是什么意思
- 茶陵古城墙是什么意思
- 茶陵复水蒜是什么意思
- 茶陵大蒜是什么意思
- 茶陵州是什么意思
- 茶陵州学是什么意思
- 茶陵州志是什么意思
- 茶陵干姜是什么意思
- 茶陵派是什么意思
- 茶陵诗派是什么意思
- 茶陵陈家大屋是什么意思
- 茶陵龙家牌坊是什么意思
- 茶青是什么意思
- 茶青色是什么意思
- 茶靠把是什么意思
- 茶面子是什么意思
- 茶鞭是什么意思
- 茶颠是什么意思
- 茶风是什么意思
- 茶食是什么意思
- 茶食店是什么意思
- 茶食蛎是什么意思
- 茶餅是什么意思
- 茶餐厅是什么意思
- 茶饭是什么意思