菱形的判定

---

注意 1．对角线互相平分与平行四边形是等价的，不能同时出现，否则重复．

2．菱形的两条对角线把菱形分成四个全等的直角三角形．

例1 如图，在菱形ABCD中，∠ABC=60°，AC=4，则BD的长为( )．

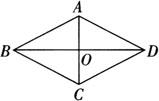
答 B．

[解析] ∵四边形ABCD是菱形，AC=4，∠ABC=60°．

∴OA=2，∠ABD=30°，∠AOB=90°．

(菱形的对角线互相垂直平分，一条对角线平分一组对角)

∴在Rt△AOB中，．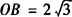

∴．

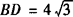(含30°角直角三角形三边之比为1∶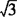∶2)

例2 菱形的一个内角等于120°，过这个角的对角线长为8cm，则这个菱形的周长为＿＿cm．

答 32．

[解析] 菱形的一个内角120°，则它的邻角60°，有一个角是60°的菱形，短对角线把菱形分成2个正三角形，即短对角线等于菱形的边长．

例3 如图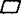，ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F．试说明四边形AFCE是菱形．

证明：∵ABCD，

∴AD∥BC．∴∠EAC=∠FCA．

又∵EF垂直平分AC，∴∠AOE=∠COF=90°，

OA=OC，

∴△AOE≌△COF．

∴AE=CF．

∴四边形AECF为平行四边形．

又EA=EC．(垂直平分线上的点到线段两端距离相等)

∴四边形AECF为菱形．

[解析] 另外证出△AOE≌COF后也可以得到OE=OF，马上就可以判断四边形AFCE为菱形．(对角线互相垂直平分的四边形是菱形)

例4 如图所示，两条等宽的纸条倾斜地重叠著，则其重叠部分ABCD是什么四边形?

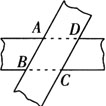
证明你的结论．

答 菱形．

首先根据两组对边分别平行的四边形是平行四边形，判定四边形ABCD是平行四边形．其次，根据平行四边形的面积等于底乘以高，因为两个纸条等宽，所以邻边AB与BC相等．根据一组邻边相等的平行四边形是菱形．判定四边形ABCD为菱形．