经典集合论

---

德国数学家康托(Georg Cantor1845－1918)创始的一种数学理论。

经典集合论用数学方法研究一般的集合，特别是无穷集合，得到了许多重要的结果，并提供了一整套处理集合的方法，对近代数学的发展作出了巨大的贡献。现在，康托的集合论已经成为数学各分支的基本工具之一，得到广泛的应用。

康托将集合定义为“一些确定的，彼此有区别的，具体的或抽象的事物的整体。”康托把构成集合的物体称为集合的元素。

现在通常用X_εA表示X是集合A的元素，X是A的元素有时也说成X属于A。为了理论的发展，康托集合论还考虑一个特殊的集合——空集，空集没有元素，常用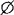表示空集。

集合之间的初等关系和运算 我们称集合A是集合B的子集，如果A的每个元素都是B的元素，用符号表示为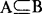。称集合A与集合B相等，如果A与B有完全一样的元素。

集合之间的初等运算主要有下列几种。

1．并运算 设A与B是集合，由A与B的一切元素组成的集合，称为集合A与B的并集。我们用A∪B表示A与B的并，因此X_εA∪B当且仅当X_εA或者X_εB。

2．交运算 集合A与集合B的交，是由A与B的公共元素构成的集合，我们用A∩B表示A与B的交集。

因此XεA∩B当且仅当X_εA并且X_εB。

3．集合的差 集合A与集合B的差集，是由所有属于A并且不属于B的元素构成的集合。A与B的差集用符号表示为A－B。因此X_εA－B当且仅当X属于A并且X不属于B。

下面是关于集合的初等运算的最基本的规律：

(1)交换律 A∪B=B∪A，A∩B=B∩A；

(2)结合律 A∪(B∪C)=(A∪B)∪C，

A∩(B∩C)=(A∩B)∩C；

(3)幂等律 A∪A=A，A∩A=A；

(4)德·摩根律 A－(B∪C)=(A－B)∩(A－C)，A－(B∩C)=(A－B)∪(A－C)；

(5)分配律 A∩(B∪C)=(A∩B)∪(A∩C)，

A∪(B∩C)=(A∪B)∩(A∪C)

除了集的初等理论，康托还发展了基数理论和序数理论，请读者参见相应的条目。