二元对比排序方法

---

模糊排序中最常用的方法。

所谓排序是针对某种特定含义进行的。例如，在人群中按健康程度排序就是一个典型的模糊排序的例子。二元对比排序，是指对几个特定的排序对象在两面对比的基础上所做的整体排序。

常用的二元对比排序方法是择优比较法；优先关系定序法；相对比较法和对比平均法。

(1)择优比较法。它源于心理学。

例如：问：在桂花、牡丹花，梅花中按“喜欢”的含义排序。此时论域U=｛桂花，牡丹花，梅花｝选几个人，每人被试m次。回答：｛佳花，牡丹花｝｛桂花，梅花｝，｛牡丹花，梅花｝三组中优越者，记录总次数。优选总和数大的先排。从而得到整体排序。

(2)优先关系定序法。

一般地表述如下

设U=｛u₁，u₂，…，u_n｝。

先建立U中任二个元素之间的优先关系。用C_ij表示u_i与u_j之间u_j优于u_j的成分(或u₁对u_j的优先选择比)。要求：

C_ii=0 0≤C_ij≤1 且，

C_ij+C_ji=1

C_ii=0表示u_i较u_j的优越程度为0。

0≤C_ij≤1表示二个元素比较的优先选择比最大为1(绝对优先)，最小为0(绝对不优先)

C_ij+C_ji=1表示二个元素优劣是互补的。

称矩阵C=(C_ij)_n×n为优先关系矩阵。

具体作法是：

(a)利用二元对比写出优先关系矩阵C=(C_ij)_n×n

(b)取阈值λ∈〔0，1〕求得截割矩阵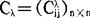

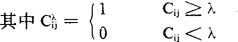
故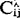是布尔矩阵。

(c)将λ由1到0递减选取得到布尔矩阵序列，当首次出现第i行元素除对角线外全为1时，则ui即为最优排序元素。

(d)除去最优排序元素得到n－1阶矩阵重复以上步骤，即得整体排序结果。

(3)相对比较法。

一般表述如下：

设有u₁，u₂，…，u_n需排序。先在任二个元素中u_i，u_j中建立比较级。

再通过一定的规则进行整体排序。

u_i，u_j的比较级定义为数对：

(f_ui(u_i)，f_ui(u_j))

且f_ui(u_i)≥0 f_ui(u_j)≤1

该数对可以这样解释：

若f_uj(u_i)表示u_i与u_j比较具有某特性的程度，则u_i与u_i比较就应具有某特性的程度是f_uj(u_j)。

排序规则如下：

(a)建立相及矩阵F=(f(u_i／u_j))_n×n

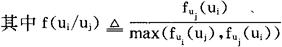
f(u_i／u_i)=1 故F矩阵对角线全为1。

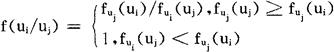
(b)按F矩阵每行取最小值，比较每行最小值由大到小进行整体排序。

(4)对比平均法。一般表述如下：

设论域U，建立笛卡儿积U×U到〔0，1〕上的映射，g：U×U→〔0，1〕

此处g实际上是表示模糊关系的二元函数。设元素u_i，u_j具有模糊关系g(u_i，u_j)和g(u_j，u_i)。

可以将它们取为：

；

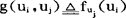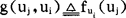
将可利用上面相对比较法排序。

也可将它们取为：

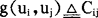g(u_j，u_i)=c_ji

则可利用上面的优先关系法排序。

更一般地说：

若在论域U中存有某种含义上的测度σ(u)而且满足归一化条件

∫_udσ=1

则可使用论域上的积分：

f(u_i／U)=∫ug(u_i／u)dσ_u (u遍历论域)

求出f(u₁／U)，f(u₂／U)，…f(u_n／u)

并依据 f(u_i／U)的大小排序。