直觉主义(逻辑)

---

本世纪初，在关于数学基础的讨论中，形成了几个不同的学派。

直觉主义逻辑是其中之一，代表人物是荷兰数学家布劳维尔。

直觉主义逻辑的数学观基本上承袭了康德的理论，主张数学来源于“直觉的先验形式”，即时间。直觉主义逻辑认为，数学是创造性的精神活动，是心灵的构造。数学独立于逻辑和语言。数学的基础在于一种先验的初始直觉。这种直觉使人认识到作为“知觉单位”的一，然后通过不断的“联结”，创造了有穷数以及无终止的无穷序列，并从而构造出各种数学对象。

根据这种观点，直觉主义逻辑，否认封闭的、已完成的实无穷的存在，在它看来，无穷只是无限增长的可能，是一个永无休止的创造过程。

传统形式逻辑的排中律断定，任一命题，或者是真的，或者是假的。

直觉主义逻辑否认排中律是普遍有效的。它认为，传统逻辑处理的是对有穷事物的思维，但是，有穷事物的规律不见得就是无穷事物的规律。例如，在有穷范围内，整体大于部份；但在无穷范围内，整体可以等于部份。在直觉主义逻辑看来，能够证明的为真；能够否证或其否定可证的为假；不可证且不可否证的，为“不可解”。

因此，排中律不普遍有效。例如命题

“π的小数表达式中有七个连续的7”，我们可能既不能证明它，也不能否证它，因此它可能既不真，也不假，而属于“不可解”。

否认排中律不仅对传统逻辑，而且对古典数学都有重大影响，因为古典数学中许多证明都引用排中律、如排中律不普遍有效，这些证明就失去了根据。

直觉主义逻辑持构造主义的观点，认为数学领域里的一切对象，例如函数、集合等等，必须可构造才能算是存在的，数学存在等于可构造。所谓可构造就是，或者能具体地给出或者能给出一个可以得到某一对象的计算方法。构造主义不承认间接的存在证明，因此也不承认不能具体给出的纯存在定理，根据这一观点，古典数学的许多纯存在证明都是不能成立的。

直觉主义逻辑是根据直觉主义的原则和方法构造的。直觉主义逻辑系统有一些区别于经典逻辑系统的地方，例如，排中律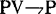在其中不成立，双重否定原则的一方可以成立，即

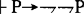
但是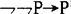，“”不是定理。

另外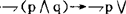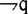也不是定理。