1.画出二次函数y=ax2+bx+c(a≠0)的图象.
2.观察图象与x轴的交点,如果有交点,交点的横坐标即为一元二次方程ax2+bx+c=0的根
注意 1.用图象求一元二次方程的根只是近似根,要用“≈”.
2.如果没有特别要求,近似根只取到十分位.
3.二次函数y=ax2+bx+c的图象与x轴的交点个数:
(1)有两个交点,则一元二次方程ax2+bx+c=0有两个不相等的实数根.
(2)有一个交点,则一元二次方程ax2+bx+c=0有两个相等的实数根
(3)没有交点,则一元二次方程ax2+bx+c=0没有实数根
例1 一元二次方程-1/2x2-3x-5/2=0的两个根是x1=-1,x2=-5,那么二次函数y=-1/2x2-3x-5/2与x轴的交点坐标是__.
答 (-1,0),(-5,0).
例2 二次函数y=x2+2x-8与x轴的交点坐标是(-4,0),(2,0).则一元二次方程x2+2x-8=0的根是_
答 x1=-4,x2=2.
例3 求二次函数y=x2-2x-1的图象与x轴的交点坐标,并求出两交点间距离.
解 方程x2-2x-1=0的根是x=1±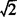 .
.
∴交点坐标是(1-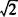 ,0),(1+
,0),(1+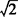 ,0).
,0).
∴交点间的距离是2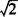 .
.
- 将来要应验的预言预兆是什么意思
- 将来进行时是什么意思
- 将果了儿是什么意思
- 将某事物搁置起来,不予重视是什么意思
- 将校是什么意思
- 将案子提交仲裁是什么意思
- 将次是什么意思
- 将欲是什么意思
- 将欲出仕是什么意思
- 将欲取之,必先与之是什么意思
- 将欲取之,必先予之(《战国策·魏策一》)是什么意思
- 将欲取之,必固与之是什么意思
- 将欲取之,必姑与之是什么意思
- 将欲夺之,必固与之是什么意思
- 将欲夺之,必固予之是什么意思
- 将欲守之,必固与之是什么意思
- 将欲安边,先宜积谷是什么意思
- 将欲废之,必固兴之是什么意思
- 将欲废之,必固兴之;将欲夺之,必固与之。是什么意思
- 将欲废之,必固兴之;将欲夺之,必固与之;将欲翕之,必固张之;将欲弱之,必固强之。是什么意思
- 将欲弱之,必固强之是什么意思
- 将欲歙之,必固张之是什么意思
- 将欲治人,必先治己是什么意思
- 将欲茂枝叶,必先救根株是什么意思
- 将欲败之,必姑辅之。是什么意思
- 将欲败之,必姑辅之。将欲取之,必姑与之是什么意思
- 将止的雨是什么意思
- 将正兵勇是什么意思
- 将正本送存档案库是什么意思
- 将武器施加于人是什么意思
- 将死是什么意思
- 将死不发丧,稳定军心败氐军是什么意思
- 将死鼓是什么意思
- 将母来谂是什么意思
- 将比是什么意思
- 将气签是什么意思
- 将水洗水是什么意思
- 将治大者,不治小;成大功者,不小苛是什么意思
- 将活人收入棺材是什么意思
- 将浓年儿是什么意思
- 将游大梁 - 洪升是什么意思
- 将滚水是什么意思
- 将漕县令是什么意思
- 将火寻远泉,煮茶傍寒松。是什么意思
- 将灵柩车上的灵柩放入墓穴之中是什么意思
- 将烟草点燃,可以多漫长是什么意思
- 将煞是什么意思
- 将熄灭的火是什么意思
- 将熔化的金属注入模型铸造是什么意思
- 将燃尽的烛是什么意思
- 将爱是什么意思
- 将爱体是什么意思
- 将爷是什么意思
- 将物体挨近火使熟或干燥是什么意思
- 将物体挨近火或置于火上是什么意思
- 将物弯曲使断开是什么意思
- 将物拟人是什么意思
- 将犯人从腰部斩为两截是什么意思
- 将犯人打死是什么意思
- 将狗比人是什么意思