概率论中引进的最重要的变换。
概率论中的许多问题,尤其那些连系著独立随机变数求和的问题,可以借助特征函数得出简单的解法。这种函数变换理论最初由法国数学家Fourier引进,在许多数学分支中起了重大作用。特征函数在解决概率论中著名的“大数定律”及“中心极限定理”时起了举足轻重的作用。
设ξ是定义在概率空间(Ω,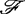 ,P)上的随机变量,其分布函数为Fξ(x),则ξ的特征函数定义为
,P)上的随机变量,其分布函数为Fξ(x),则ξ的特征函数定义为
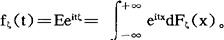
对于非负整值随机变量,若其母函数为P(S)(见“母函数”条),其特征函数为f(t),则f(t)=p(eit)。
对于连续型随机变量,若其分布密度为p(x),则其特征函数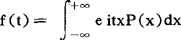 ,这时,特征函数即为密度函数p(x)的Fourier变换。
,这时,特征函数即为密度函数p(x)的Fourier变换。
设特征函数f(t)对应于分布函数F(x),x1x2是F(x)的连续点,则有
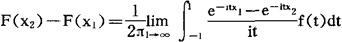
由此可知,分布函数由特征函数唯一确定。这样,对分析性质比较差的分布函数的研究即可由分析性质比较好的特征函数的研究所取代。
以下是特征函数的主要性质:
a.特征函数在全直线上一致连续,且满足:f(o)=1,|f(t)|≤1 (-∞ b.两个独立随机变量之和的特征函数等于其特征函数之积。 c.如果随机变量ξ有n阶绝对矩,则ξ的特征函数f(t)可微分n次,且当k≤n时,f(k)(0)=ikEξk。 下面给出几个重要分布的特征函数: 二项分布b(k;n,p):f(t)=(peit+q)n; 普阿松分布p(k;λ):f(t)=eλ(eit-1); 高斯分布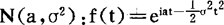 。
。
- 乘云是什么意思
- 乘云气飞行是什么意思
- 乘云绣是什么意思
- 乘云行泥是什么意思
- 乘云雾飞行是什么意思
- 乘云驾鹤是什么意思
- 乘人是什么意思
- 乘人不备入室行窃是什么意思
- 乘人不备暗中射出的箭是什么意思
- 乘人不备而杀害是什么意思
- 乘人不备进行杀害是什么意思
- 乘人不虞是什么意思
- 乘人之不及 攻其所不戒是什么意思
- 乘人之危是什么意思
- 乘人之危加以陷害是什么意思
- 乘人之危抨击是什么意思
- 乘人之危的民事法律行为是什么意思
- 乘人之危,协助别人做害人的事是什么意思
- 乘人之危;落井下石是什么意思
- 乘人之厄是什么意思
- 乘人之急是什么意思
- 乘人之约,非仁也。是什么意思
- 乘人之车者载人之患是什么意思
- 乘人之车者载人之患,衣人之衣者忧人之忧,食人之食者死人之事。是什么意思
- 乘人之车者,载人之患;衣人之衣者,忧人之忧;食人之食者,死人之事是什么意思
- 乘人危急之时加以陷害是什么意思
- 乘人危难,加以陷害是什么意思
- 乘人受难时一齐打击是什么意思
- 乘人有危难时加以陷害是什么意思
- 乘人没有料到而采取行动是什么意思
- 乘人车,载人息是什么意思
- 乘众人之智者,即无不任也;用众人之力者,即无不胜也是什么意思
- 乘众人之智,则无不任也;用众人之力,则无不胜也是什么意思
- 乘伙着是什么意思
- 乘传是什么意思
- 乘伪行诈是什么意思
- 乘住是什么意思
- 乘便是什么意思
- 乘便,利用有利时机是什么意思
- 乘便,顺便是什么意思
- 乘倒是什么意思
- 乘傳是什么意思
- 乘兴是什么意思
- 乘兴任情是什么意思
- 乘兴南游不戒严,九重谁省谏书函。是什么意思
- 乘兴南游不戒严,九重谁省谏书函。 春风举国裁宫锦,半作障泥半作帆。是什么意思
- 乘兴坐胡床是什么意思
- 乘兴嫌太迟,焚却子猷船。是什么意思
- 乘兴山阴是什么意思
- 乘兴棹是什么意思
- 乘兴泛舟是什么意思
- 乘兴泻、云液落新荷,休辞醉。是什么意思
- 乘兴溱洧沐恩波,匕命倍主入觐多;鹭序鸳行均幼弱,图书万国不羞讹(打古人名四)车济、侯朝、珧稚、文同是什么意思
- 乘兴空还是什么意思
- 乘兴而作是什么意思
- 乘兴而去是什么意思
- 乘兴而来是什么意思
- 乘兴而来兴尽而返(打药名一)王不留行是什么意思
- 乘兴而来,兴尽而归是什么意思
- 乘兴而来,兴尽而返是什么意思