活动分析

---

在生产可能性集合的结构分析的基础上，对生产过程进行研究称活动分析。

设Y为生产可能性集合，则y∈Y就是一个可行的生产计划。在活动分析中称y为一个(生产)活动或生产过程。对一个具有n种物品的经济，y中的负分量y_i＜0表示第i种物品为(纯)生产要素，正分量y_j＞0表示第j种物品为(纯)产出，如果y_k=0则表示这个活动本质上与第k种物品无关。

在活动分析中通常设生产可能性集合Y满足如下假定。

(1)比例性：y∈Y和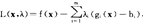α≧0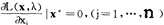αy∈Y。这意味著生产是规模报酬不变的，且各种物品是完全可分的。

(2)可加性：y∈Y和y′∈Y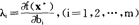y+y′∈Y，这意味著生产活动之间无交互影响。

(3)不能无中生有性：y≧0#y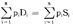Y，这意味著没有正的投入不能有正的产出。

如果在Y中存在m个活动a_i=(a_i1，…，a_in)，i=1，…，m，使得Y中任何一个活动y都可写成y=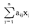λ_ia_i，λ_i≧0，则称这m个活动{a_i}为基础活动，λ_i为y的第i个基础活动的水平。

在此情形，如把a_i作为第i列而构成一个n×m矩阵A，则称A为技术矩阵。这时，生产可能性集合Y可写成Y={y|Aλ=y，λ≧0}。

对y°∈Y，如果不存在y∈Y使得y≧y°且y≠y°，则称y°为Y中的一个优效过程，又称优效点。

关于优效过程有如下的定理：y°是Y中的优效过程的必要且充分条件是存在一个正向量p=(p₁，…，p_n)，使得对所有y∈Y都有p·y°≧p·y。

当可能使用的生产要素有一定限制时，设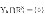_i为第i种物品的最大可能投入量，记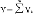=(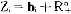₁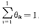，…，_n)，则生产要素有限制的生产可能性集合为Y_F={y|Aλ=y，λ≧0，y+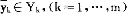≧0}。对任何一个正向量p，如果线性规划问题：

maxp·y=max(pA)·λ

s．t．Aλ+#≧0

λ≧0

有解λ^*，则y^*=Aλ^*是Y_F的一个优效过程。通过变动p，就可得到Y_F的优效过程的集合，人们在选择生产过程时，当然是在优效过程集合中选择符合其他标准的过程。