1.余弦定理的适用题型.
❶ 已知三边,求三角.
❷ 已知两边及其夹角,求第三边.
2.正弦定理的适用题型
❶ 已知两角及一边,求其余的边和角.
❷ 已知两边和一边所对的角,求其余的边和角.
但此种类型有多解的情形,具体解的情况举例说明.
如已知a,b和A求B时,解的情况如下:
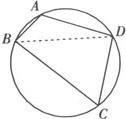
A为锐角时,1°a 2°a=bsinA,一解. 3°bsinA 4°a≥b,一解. A为直角或钝角时,1°a≤b,无解. 2°a>b,一解. 例1 在△ABC中,已知c4—2(a2+b2)c2+a4+a2b2+b4=0,求角C. 分析 将关于三边的等式进行适当变形,利用余弦定理求角. 例2 在△ABC中,已知 分析 这是已知两边一对角解三角形的问题,可用正弦定理求解,但先要判定△ABC是否有解,有几解,亦可用余弦定理求解. 解 ∵B=45°<90°,且b 由正弦定理得 例3 已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积. 解 如图,连结BD,则有四边形ABCD的面积 由余弦定理,在△ABD中 BD2=AB2+AD2—2AB·ADcosA =22+42—2×2×4cosA =20—16cosA. 在△CDB中, BD2=CB2+CD2—2CB·CDcosC =62+42—2×6×4cosC =52—48cosC. ∵20—16cosA=52—48cosC, ∵cosC=—cosA, ∴64cosA=—32,cosA=—1/2. ∴A=120°,∴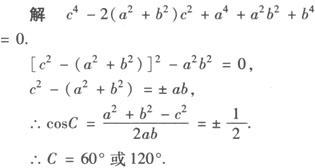
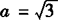 ,
,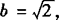 ,B=45°,求A、C和c.
,B=45°,求A、C和c.
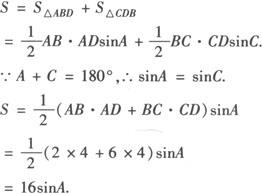
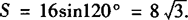 .
.
- 华佗是什么意思
- 华佗是什么意思
- 华佗是什么意思
- 华佗是什么意思
- 华佗是什么意思
- 华佗是什么意思
- 华佗是什么意思
- 华佗(huà—)(?—208)是什么意思
- 华佗之死是什么意思
- 华佗五禽是什么意思
- 华佗传说是什么意思
- 华佗再造丸是什么意思
- 华佗出师是什么意思
- 华佗出蛇是什么意思
- 华佗医死人是什么意思
- 华佗和白芍是什么意思
- 华佗处方骂贪官是什么意思
- 华佗夹脊是什么意思
- 华佗庵是什么意思
- 华佗故居是什么意思
- 华佗救脱阳方是什么意思
- 华佗救脱阳方是什么意思
- 华佗散是什么意思
- 华佗散是什么意思
- 华佗珍珠泉是什么意思
- 华佗琼林寺学医是什么意思
- 华佗的传说是什么意思
- 华佗的打老儿丸是什么意思
- 华佗神医秘传是什么意思
- 华佗神医秘传是什么意思
- 华佗神医秘传是什么意思
- 华佗神医秘传是什么意思
- 华佗笑传是什么意思
- 华佗药枕是什么意思
- 华佗解围是什么意思
- 华佗赤散是什么意思
- 华佗青囊是什么意思
- 华佛综合征是什么意思
- 华佛综合征是什么意思
- 华侈是什么意思
- 华侨是什么意思
- 华侨是什么意思
- 华侨·华人问题论文集是什么意思
- 华侨、归侨、侨眷的权利和利益是什么意思
- 华侨不变论是什么意思
- 华侨与中国革命是什么意思
- 华侨与华人是什么意思
- 华侨与国内公民婚姻的规定是什么意思
- 华侨与外籍华人是什么意思
- 华侨与抗日战争是什么意思
- 华侨与抗日战争是什么意思
- 华侨与爪哇人民联合起义是什么意思
- 华侨中心之南洋是什么意思
- 华侨事务委员会是什么意思
- 华侨(人民币)定期储蓄是什么意思
- 华侨人物志是什么意思
- 华侨企业是什么意思
- 华侨企业是什么意思
- 华侨公报是什么意思
- 华侨兴业公司是什么意思