数列a1,a1q,a1q2,…(|q|<1)前n项的和,当n无限增大时的极限,叫做这个无穷递缩等比数列各项的和,记为S,即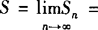
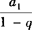 .
.
例1 (1)使lim(2x+1)n=0成立的实数x的取值范围是____.
(2)使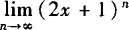 存在的实数x的取值范围是____.
存在的实数x的取值范围是____.
解 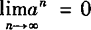 成立
成立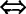 —1
—1
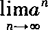 存在
存在 —1
—1
(1)依题意有—1<2x+1<1,解得—1 ∴x的取值范围是(—1,0). (2)依题意有—1<2x+1≤1,即—1 ∴x的取值范围是(—1,0]. 例2 对于数列{an}若 A.❶ ❷ B.❶ ❸ C.❷ ❹ D.❸ ❹ 故选C 探索延拓创新 例3 比较1与0.9的大小.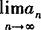 =0,则称数列{an}为无穷小数列,在下列各数列中为无穷小数列的是( ).
=0,则称数列{an}为无穷小数列,在下列各数列中为无穷小数列的是( ).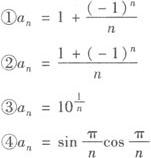
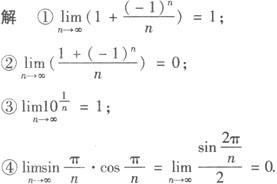
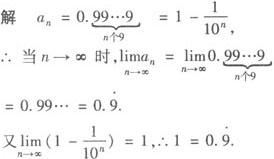
- 捡口角子是什么意思
- 捡喝皮是什么意思
- 捡嘴是什么意思
- 捡嘴儿是什么意思
- 捡囝是什么意思
- 捡地是什么意思
- 捡场是什么意思
- 捡场的是什么意思
- 捡埋是什么意思
- 捡好是什么意思
- 捡娃儿是什么意思
- 捡子子是什么意思
- 捡小孩是什么意思
- 捡小菜是什么意思
- 捡屎是什么意思
- 捡平顺是什么意思
- 捡式是什么意思
- 捡彩族是什么意思
- 捡得是什么意思
- 捡得一根针,带掉一斤铁是什么意思
- 捡手是什么意思
- 捡押是什么意思
- 捡抽是什么意思
- 捡拢是什么意思
- 捡括是什么意思
- 捡拾是什么意思
- 捡拾压捆机是什么意思
- 捡拾器是什么意思
- 捡拾装置是什么意思
- 捡拾集垛机是什么意思
- 捡捡拆拆是什么意思
- 捡摊子是什么意思
- 捡日子是什么意思
- 捡旧是什么意思
- 捡木子是什么意思
- 捡来的麦子打烧饼——没本儿是什么意思
- 捡来的麦子打烧饼卖是什么意思
- 捡果儿是什么意思
- 捡果子茶是什么意思
- 捡查校正是什么意思
- 捡柴是什么意思
- 捡样子是什么意思
- 捡根芭茅花就杀进大营是什么意思
- 捡正是什么意思
- 捡洋捞是什么意思
- 捡洋落儿是什么意思
- 捡淤是什么意思
- 捡漏是什么意思
- 捡漏儿是什么意思
- 捡烂择儿是什么意思
- 捡煤核儿是什么意思
- 捡猪屎是什么意思
- 捡瓦是什么意思
- 捡生是什么意思
- 捡生娘是什么意思
- 捡生婆是什么意思
- 捡直是什么意思
- 捡相因是什么意思
- 捡着是什么意思
- 捡破烂是什么意思