对称问题

---

1．点关于直线对称问题

(1)点(a，b)关于点(x，y)的对称点坐标为(2x—a，2y—b)．

(2)点(a，b)关于x轴，y轴，原点，直线y=x，直线y=—x的对称点分别为(a，—b)，(—a，b)，(—a，—b)，(b，a)和(—b，—a)．

(3)点A(x，y)关于直线x+y+c=0的对称点A′的坐标为(—y—c，—x—c)．

(4)点A(x，y)关于直线x—y+c=0的对称点A′的坐标为(y—c，x+c)．

(5)曲线f(x，y)=0关于直线x+y+c=0的对称曲线为f(—y—c，—x—c)=0．

(6)曲线f(x，y)=0关于直线x—y+c=0的对称曲线为f(y—c，x+c)=0．

2．若P，Q两点关于直线l成轴对称，则PQ的中点在直线l上且

k_pO·k=—1(若PQ斜率存在)

3．曲线C∶f(x，y)=0与曲线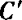∶g(x，y)=0关于点P(a，b)对称，则曲线C′上任一点M′(x，y)，关于P的对称点M(2a—x，2b—y)在曲线C上，即

g(x，y)=f(2a—x，2b—y)．

4．曲线C：f(x，y)=0关于直线y=kx+b的对称曲线C′，则C′上任一点P关于直线y=kx+b对称的点必在曲线C上，即曲线关于直线的对称问题转化为点关于直线的对称问题．

例1 求点P(2，—1)关于点(3，4)的对称点坐标．

分析 利用中点坐标公式．

解 设对称点P′(x，y)，

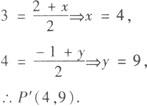
点评 将点关于点对称问题转化为线段中点问题

例2 求点A(2，2)关于直线l∶2x—4y+9=0的对称点的坐标．

分析 两点A、B关于直线l对称，即为AB⊥l，垂足M为线段AB中点．

解 设对称点B(a，b)

∵直线l的斜率存在且不为0，

∴直线AB的斜率存在，

将❶ ❷ 联立解得：a=1，b=4，

∴对称点B(1，4)．

例3 已知直线l∶3x—y+3=0．

求：(Ⅰ)直线l关于点P(4，5)的对称线；

(Ⅱ)直线x—y—2=0关于直线l的对称直线方程．

解 (Ⅰ)在直线l∶3x—y+3=0上取两点：

A(—1，0)，B(0，3)，

则A、B两点关于点P(4，5)的对称点为A′(9，10)，B′(8，7)．

由两点式过A′，B′的直线为

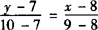
即 3x—y—17=0．

(Ⅱ)联立两直线方程得

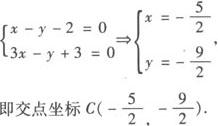
又∵直线x—y—2=0的斜率k₁=1，

直线l的斜率k₂=3．

设所求对称直线斜率为k，

由到角公式有：

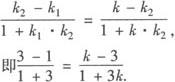
解得k=—7由点斜式所求对称直线的方程为y+9/2=—7(x+5/2)，

即7x+y+22=0．