对偶单纯形法

---

利用对偶问题的有关性质来求解线性规划模型的一种方法。

具体步骤如下：

第一步：模型标准化，填充初始单纯形表格。为了使用这种算法，必须是对偶问题可行，原问题不可行。

因此，填充的初始表中，必须是所有Z_jC_j≥0及存在有b_i＜0。

第二步：选择b₁＜0中，其绝对值最大的元素所在行为标准行，对应这个行的基变量就是出基变量，并作标记*。

第三步：对标准行i*中具有负元素的那些列，由下式计算比值：

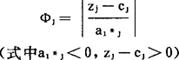
选择最小列比值min｛Φ_j｝所在列为标准列，对应这个列的非基变量就是进基变量。

第四步：对确定好的进基变量和出基变量进行代换，按一般原始单纯形运算表中介绍的方法，进行迭代运算，得到新的单纯形表。

第五步：如果所有的b_i≥0，停止迭代过程，写出最优解。否则，返回第二步。

例用对偶单纯形法求解

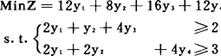
y₁，y₂，y₃，y₄≥0

约束条件标准化：

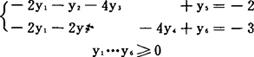
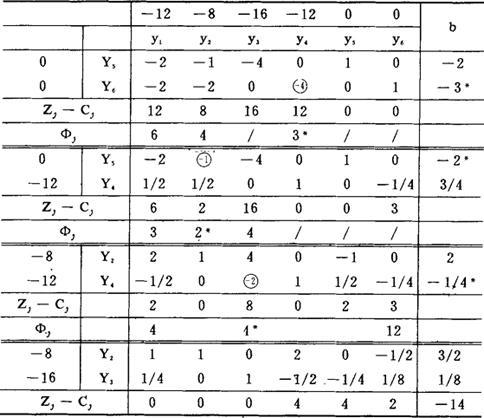
得到最优解：y₁^*=0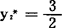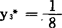，，，y₄^*=0，Z^*=14。

(此例中，从最终单纯表看到，非基变量Y₁的检验数为零，故本例是一个多重最优解问题)