奇函数和偶函数的性质

---

1．定理：奇函数的图象是关于原点成中心对称，偶函数的图象是关于y轴的轴对称图形．反过来，如果一个函数的图象关于原点成中心对称图形，那么这个函数是奇函数；如果一个函数的图象关于y轴成轴对称图形，那么这个函数是偶函数．

2．若偶函数f(x)在区间[a，b](a>0)是增(减)函数，则f(x)在[—b，—a]上是减(增)函数，反之也成立；若奇函数f(x)在区间[a，b](a>0)是增(减)函数，则f(x)在[—b，—a]上是增(减)函数，反之也成立．

3．若奇函数f(x)在点x=0处有意义，则f(0)=0．

判断函数奇、偶性的方法

1．定义法

第一步

求f(x)定义域，若定义域不关于原点对称，则f(x)不具有奇偶性，若定义域关于原点对称，不一定具有奇偶性，需进行下一步．

第二步

计算f(—x)∶

若f(—x)=f(x)，则f(x)为偶函数；

若f(—x)=—f(x)，则f(x)为奇函数；

若f(—x)≠f(x)，且f(—x)≠—f(x)，

则f(x)为非奇非偶函数．

2．图象法，若图象关于原点对称，则函数为奇函数，若图象关于y轴对称，则函数为偶函数．

例1 判断下列函数的奇偶性．

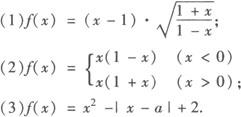
分析 根据奇函数、偶函数的定义判断．

解 (1)选确定函数的定义域，由于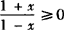，得—1≤x<1，其定义域不对称于原点，所以f(x)既不是奇函数也不是偶函数．

(2)方法一 ∵函数f(x)的定义域是(—∞，0)∪(0，+∞)，并且当x>0时，—x<0，

∴f(—x)=(—x)[1—(—x)]

=—x(1+x)=—f(x)(x>0)；

当x<0时，—x>0，

∴f(—x)=—x(1—x)=—f(x)(x<0)．

故函数f(x)为奇函数

方法二∵f(x)=x(1+|x|)(x≠0)，

∴f(—x)=—x(1+|—x|)

=—x(1+|x|)

=—f(x)．

∴f(x)为奇函数．

(3)函数f(x)的定义域为R

当a=0时，f(x)=f(—x)，∴f(x)是偶函数；

当a≠0时，f(a)=a²+2，f(—a)=a²—2|a|+2，

f(a)≠f(—a)且f(a)+f(—a)

=2(a²—|a|+2)

=2(|a|—1/2)²+7/2≠0，

∴f(x)为非奇非偶函数．

例2 设f(x)是定义在R上的偶函数，并在区间(—∞，0]内是增函数．试解关于a的不等式f(2a²+a+1)2—2a+1)．

分析 f(x)在(—∞，0]内是增函数，2a²+a+1、3a²—2a+1在(—∞，0]内吗?能否转化到(—∞，0]内呢?

解 ∵2a²+a+1、3a²—2a+1均在(0，+∞)上，

由函数的奇偶性想到—2a²—a—1<0，

—3a²+2a—1<0．

即解f(—2a²—a—1)2+2a1)，

—2a²—a—1<—3a²+2a—1，

即0