声波方程与声速公式

---

运动方程——声压与质点振速的关系：

流体受声波扰动后，单位体积内两侧面所受压力差将使该体积内质量产生加速度。由牛顿第二定律

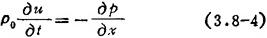
对于平面正弦波则有

p=ρ₀cu (3．8－5)

式中 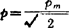，为有效声压，其中p_m是声压幅值；p₀为空气介质密度；c为空气中的声速，取Z=ρ₀o，称介质的特性阻抗；u为介质质点振速。

连续性方程一质点振速与介质密度的关系：

流体受声波扰动后，单位时间内流入流出单位体积的质量差，等于体积内质量增减或密度变化。即

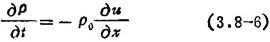
对平面正弦波则有

式中Δρ为介质密度增量。

物态方程一声压与介质密度的关系：

声波引起压力的变化与密度的变化成正比。即

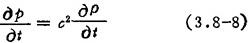
声速公式：

对于理想气体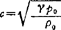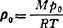，，，故声速公式为

式中 γ=1．4，为空气的比热比；R=8．31J／克分子、度，为普适气体常数；T=273．2+t，为绝对温度；M=28．8×10^－3kg／克分子，为空气分子质量。空气中声速公式可简化为

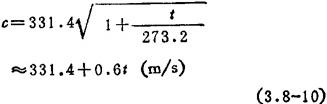
式中 t为温度(℃)。

波动方程：

由上述方程可求出声压与时间和空间坐标的关系

推广到三维空间，则

式中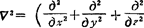)，为拉普拉斯算子。