2.2.1 应力偏量与应变偏量
应力偏量:在塑性力学中,常将应力状态分解为两部分。一部分为各向相等的压(或拉)应力,其分量为(σm,σm,σm,O,O,o),σm为平均应力,其值为
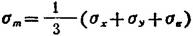
该应力状态只引起弹性的体积变形。另一部分为应力偏量,其分量为(σx-σm,σy-σm,σx-σm,τxy,τyz,τzx),常记为(Sx,Sy,Sz,Sxy,Syz,5zx),它只引起形状的改变,塑性变形只与应力偏量有关。
应变偏量:与应力分析类似,应变状态也分为两部分,即只与体积变化有关的部分(εm,εm,εm,O,O,o)和只与形状变化有关的部分(ex,ey,ez,exy,eyz,ezx)。其中,εm称为平均应变:ex=εx-em,ey=εy-εm,ez=εz-εm,
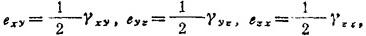
称为应变偏量。
2.2.2 塑性条件
材料进入塑性状态时应力分量必须满足的条件,称为塑性条件,或称屈服条件。
Tresca条件:当最大剪应力等于剪切屈服极限时,材料开始进入塑性状态,即
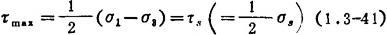
或 σ1-σ3=σ3
Mises条件:当应力强度等于材料的屈服极限时,材料开始进入塑性状态,即
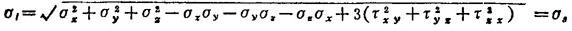
用主应力表示,则为
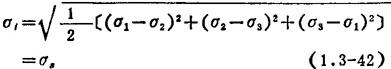
式中,σ1称为应力强度。
2.2.3 塑性应力应变关系
当材料进入塑性状态后,广义虎克定律已不适用,需要建立塑性阶段的应力应变关系。主要有两种类型:增量理论和全量理论。
增量理论:存在于应力和应变增量之间的关系。对于不同的材料模型,其关系表达式也不相同。
理想刚塑性材料的增量理论——Levy-Mises方程:
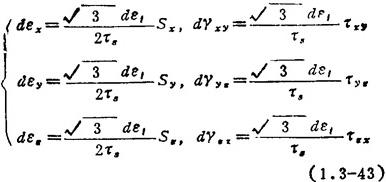
式中,de1为应变强度增量,其值为
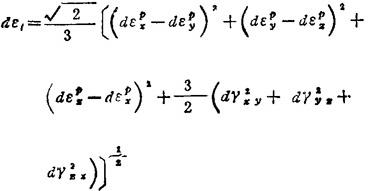
2)理想弹塑性材料的增量理论——Prandtl-Reuss方程:
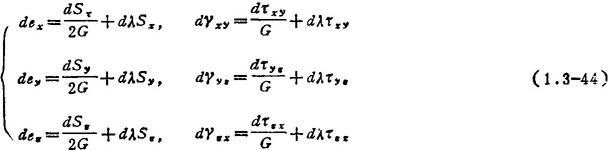
式中 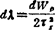 ;dWp为塑性功增量
;dWp为塑性功增量
上述各式均为加载过程中增量理论公式。而其他过程dλ=0。
(2)全量理论:在简单加载条件下,应力强度σi与应变强度εt有确定的对应关系。在弹塑性小变形的情况下,下述的伊留辛(ИnbloшиH)理论比较简便。
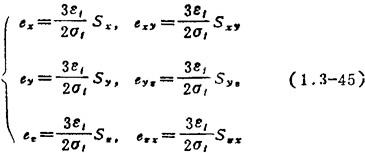
其中,应力强度σi与应变强度ε1有确定的函数关系,即σ1=Φ(ε1)。
2.2.4 弹塑性理论的基本方程和边界条件
弹塑性理论的基本方程 与弹性理论的基本方程的主要不同之处,在于物理方程的差异。
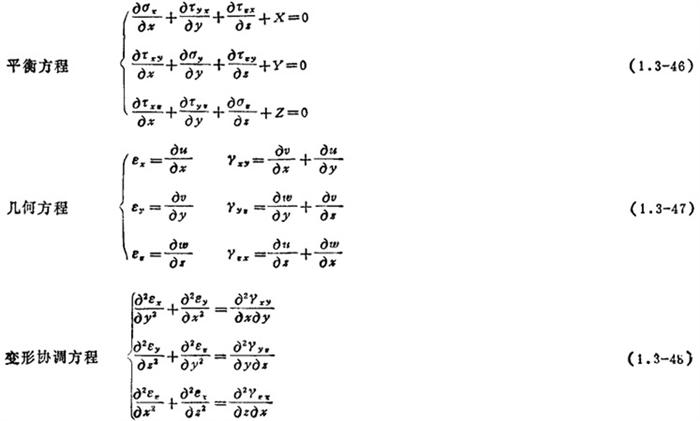
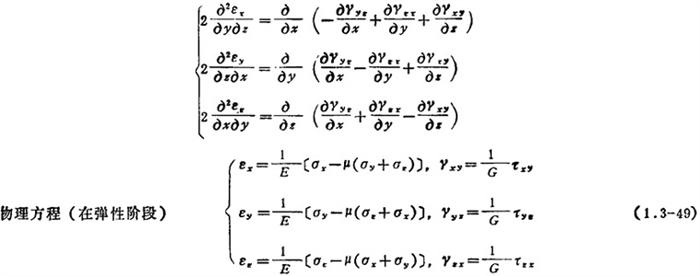
在塑性阶段,其增量理论及全量理论见(2.2.3)。
边界条件1Su上,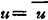 ,
,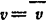 ,
,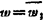 1
1
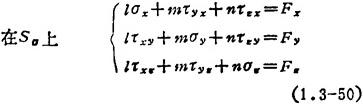
- 順是什么意思
- 順吹是什么意思
- 順天元寳是什么意思
- 順天道是什么意思
- 順布嚕是什么意思
- 順布魯是什么意思
- 順從是什么意思
- 順志是什么意思
- 順斗极是什么意思
- 順昌酒是什么意思
- 順欲是什么意思
- 順止是什么意思
- 順治通寳是什么意思
- 順治鈔貫是什么意思
- 順溜紙是什么意思
- 順濟橋是什么意思
- 順硃兒是什么意思
- 順祝是什么意思
- 順義公碑是什么意思
- 順袋是什么意思
- 順陵石獅是什么意思
- 順風耳是什么意思
- 順龍是什么意思
- 頇是什么意思
- 須是什么意思
- 須佗是什么意思
- 須卜是什么意思
- 須句是什么意思
- 須女是什么意思
- 須彌山是什么意思
- 須彌山石窟是什么意思
- 須彌座是什么意思
- 須彌福壽之廟是什么意思
- 須從是什么意思
- 須愷是什么意思
- 須摩提女緣品圖是什么意思
- 須曼那是什么意思
- 須朐是什么意思
- 須末那是什么意思
- 須眉是什么意思
- 須知是什么意思
- 須肑是什么意思
- 須臾是什么意思
- 須遂是什么意思
- 須達拏太子本生圖是什么意思
- 須部是什么意思
- 須陀食是什么意思
- 須静齋雲烟過眼録是什么意思
- 須髯是什么意思
- 須鸁是什么意思
- 須麋是什么意思
- 頉是什么意思
- 頊是什么意思
- 頋是什么意思
- 頌是什么意思
- 頌堂是什么意思
- 頌歎是什么意思
- 頌琴是什么意思
- 頌瑟是什么意思
- 頌磬是什么意思